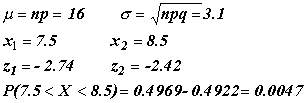|
DISTRIBUCIONES
DE PROBABILIDAD
|
ejercicios
|
| Una
distribución de probabilidad es un modelo matemático que asocia
valores de una variable aleatoria con sus respectivas
probabilidades, es decir: |
|
Probabilidad
de x
= Función de x |
|
| Las
distribuciones se caracterizan por una fórmula que determina el
tipo de distribución y por un conjunto de parámetros, que son propios de
cada espacio muestral. |
| En el caso de
una variable discreta , la distribución puede describirse mediante
una función de probabilidad, que para cada valor de x
de la variable X
determina la probabilidad de ser asumido: |
| o
bien por medio de una función de distribución de probabilidad
acumulada o simplemente función de distribución, la que, para
cada valor provee la probabilidad de no ser superado |
|
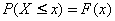
|
|
| evidentemente,
el valor de la función de distribución es igual a la suma de todos los
valores de la función de probabilidad desde el extremo inferior del
dominio de la variable
hasta x
inclusive |
| Ejemplo:
Al lanzar dos dados la suma de ambos puede asumir 11 valores
diferentes en 36 puntos muestrales |
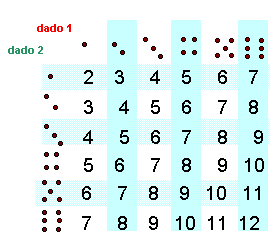 |
2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12 |
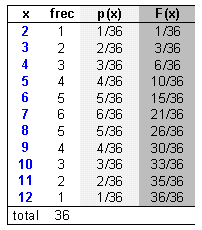 |
En
este caso vemos que la distribución de p(x) obtenida es simétrica.
|
| Para
el caso de 1 solo dado, donde todos los valores tienen la misma probabilidad de salir
(1/6), obtendríamos una distribución uniforme |
| Una
muy importante distribución de variable discreta es la Binomial
ver
experiencia de Bernouilli
|
| Esta
distribución está asociada al número de éxitos de un acontecimiento A
en un número n de ensayos cuando p = P (A), la probabilidad de A en un
sólo ensayo, permanece constante a lo largo de todo el experimento |
|
La probabilidad
de fracaso en cada ensayo permanecerá también constante y por ser A
y
|
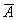
|
|
|
acontecimientos
complementarios:
|
|
q
= |
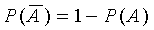 |
=
1 - p |
|
Para
que ocurran x
éxitos en n
ensayos, deben ocurrir también (n-x)
fracasos
Por lo tanto: |
|
La probabilidad de obtener x
éxitos en un orden dado de éxitos y fracasos es igual
a |
|
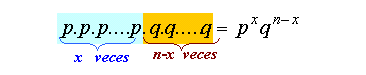
|
por
ser los acontecimientos independientes de un ensayo a otro |
| Un
mismo resultado puede ser obtenido en nCx
ordenamientos diferentes, entonces : |
|
|
|
Ejemplo:
Si la prevalencia de una enfermedad es p = 0.30. ¿Cuál
será la probabilidad de encontrar en 4 animales tomados al azar, 3
enfermos?
p = 0.30 q = 1- 0.30 = 0.70 |
| Las
diferentes formas de encontrar 3 enfermos serán: EEES, EESE, ESEE,
SEEE ( cuatro formas diferentes) o lo |
| que es lo
mismo 4C 3 = |
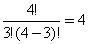 |
|
p(3) = 4 x
0.33 x 0.70 |
| Al
graficar la distribución de probabilidad se obtiene un diagrama de
bastones o espectro. La suma de todas las probabilidades parciales deberá
ser 1 (axiomas de probabilidad) |
|
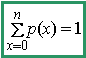
|
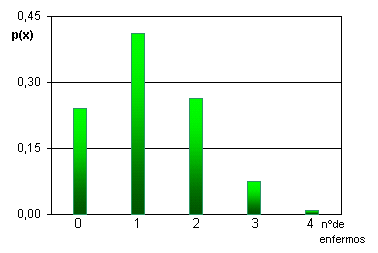 |
| p(0)
= 0.2401 |
| p(1) =
0.4116 |
| p(2) =
0.2646 |
| p(3) =
0.0756 |
| p(4) =
0.0081 |
|
S
=
1.000 |
|
|
La
probabilidad de encontrar 2 o más enfermos :
|
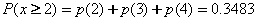 |
| Los
PARÁMETROS
de la distribución BINOMIAL son : |
n
y
p |
| La
MEDIA
de una variable binomial es: |
np |
| La
VARIANZA de
una variable binomial es |
npq |
|
| Distribución
de Poisson |
Como
distribución por si misma (variable Poisson) |
| Como
aproximación a la binomial |
| Un fenómeno en
el cual el número de veces que ocurre un acontecimiento en cualquier
intervalo de amplitud h
de un soporte
continuo (tiempo, longitud, área,etc), es una variable aleatoria,
que depende solamente de la amplitud del intervalo, recibe el
nombre de "proceso de Poisson". El promedio del número de
éxitos en cualquier intervalo será entonces = l
h donde l
es una
constante (la media de éxitos por unidad de medida del soporte) |
|
EL PARÁMETRO
de la distribución Poisson es :
|
l |
| La
MEDIA
de una variable Poisson es: |
| La
VARIANZA de
una variable Poisson es: |
|
| Como
aproximación a la Binomial : Esta
diferenciación en dos "categorías" es meramente didáctica, ya
que una de las formas de hallar la función de probabilidad del número de
éxitos en una variable Poisson es el paso al límite en la Binomial
(ver demostración)
|
Cuando n
tiende a infinito y p a cero, siendo l
= np constante, la distribución binomial puede ser
aproximada por la distribución de Poisson |
| En la
práctica, la aproximación es muy buena cuando l
<
5, siendo n
> 50 |
Ejemplo
En 60 ensayos
con p = 0.002 a) Calcular la media y la varianza |
|
b)
Calcular p( 5) |
| a)
media |
l
= np = 60 x 0.002 =0.12 |
varianza |
l
= npq = 60 x 0.002 x 0.998 = 0.12 |
| b)
p( 5) |
(
0.125 x e-0.12) / 5! =1.84 x 10-7 |
|
| Con una variable
aleatoria continua,
carece de sentido plantearse el problema de determinar cuál es la
probabilidad de que asuma un determinado valor x dado, ya que en cualquier
intervalo existen infinitos valores posibles y por lo tanto : |
|
P(x) = |
Número de casos
favorables
Número de casos posibles |
= 0 |
|
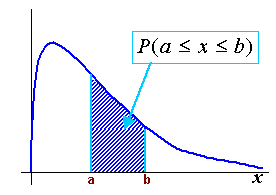
| En
consecuencia para describir la distribución de una variable continua, se
utiliza la función
de densidad
f(x),
la que proporciona la probabilidad de que x
pertenezca a un intervalo (a, b) dada como el área bajo la
curva entre a y b |
 |
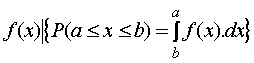 |
| Al
igual que en el caso de la variable discreta, la distribución de una
variable continua puede también ser descrita |
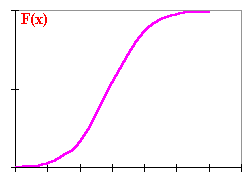
| por medio de una
función
de distribución,
F(x) que da las
probabilidades acumuladas desde |
|
|
| hasta
un valor dado de x, o sea la probabilidad de no superarlo |
Al igual que en
el caso de la variable discreta, la distribución de una variable continua
puede también ser descrita por medio de una función de distribución
, F(x) que da las
probabilidades acumuladas desde
x=
- 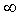 hasta un valor dado de
x
(en la figura: a), o sea la probabilidad de no
superarlo hasta un valor dado de
x
(en la figura: a), o sea la probabilidad de no
superarlo |
| La más
importante de las distribuciones continua es la distribución
normal
o de Laplace-Gauss,
tanto por la frecuencia con que se encuentra como por su aplicación
teórica |
|
La función
de densidad es:
|
sus parámetros
son: |
|
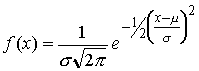
|
|
| Dado que tanto m
como s
puede asumir infinitos
valores lo que hace
impracticable tabular las probabilidades para todas las posibles
distribuciones normales, se utiliza la distribución
normal reducida o tipificada |
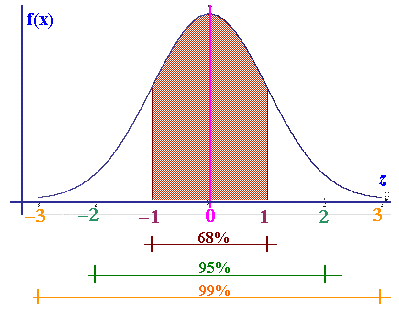
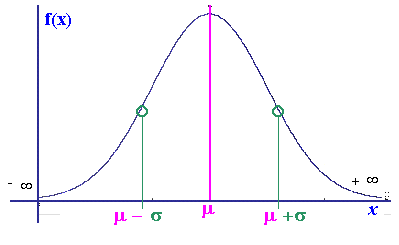
| Una regla
empírica indica que en cualquier distribución normal las probabilidades
delimitadas entre 1 desviación típica, 2 desviaciones típicas y 3
desviaciones típicas son el 68%, 95% y 99% respectivamente
Pero para valores
intermedios esta regla es insuficiente. Las probabilidades de la variable
tipificada están tabuladas para los diferentes valores de la variable
Para calcular entonces probabilidades asociadas a una curva normal
específica hay que recurrir directamente a una transformación de la
variable a otra
referida a la variable z,
tipificación de la variable en estudio |
 |
| USO DE LA
TABLA DE LA DISTRIBUCIÓN NORMAL
TIPIFICADA
Z |
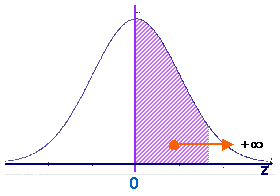 |
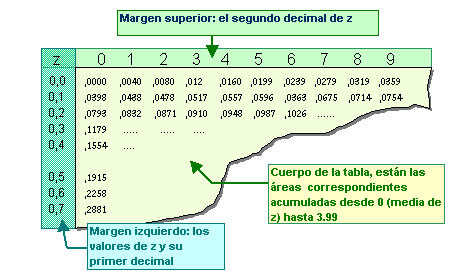
Hay muchos tipos
de tablas de la distribución normal
La que se explica aquí representa las áreas para los diferentes
valores de z desde 0 hasta +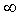
Los valores negativos de
z NO están tabulados ya que la distribución es simétrica
|
|
|
Ejemplos:
1¿Cuál es la
probabilidad de que un valor de z esté entre:
a.- 0 y 1.32
b.- 0 y -2.03
c.--2.33 y +2.03
2. Hallar P (z > 1.25)
3.Hallar P(-0.34 < z <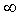 ) )
4.Hallar
P(+0.34 < z < +2.03)
5. Hallar P(-1.96 < z < +2.3)
|
Ejercicio:
a) Sea una variable distribuida normalmente con media
m
= 4 y
desviación típica s
= 1.5.¿Cuál
es la probabilidad de encontrar un valor x
> 6 ?
| b)
Hasta ahora se vio como calcular una probabilidad de acuerdo a un
valor de z dado. Pero puede surgir el problema de determinar
aquel valor de z que deja por encima o por debajo de él una
probabilidad dada.
Aquí entonces
lo que se busca es un valor de z. ¿Cuál es el valor de z que
deja por debajo de él el 5%?
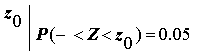 |
Se
busca en el cuerpo de la tabla 0.4500
En este caso en la tabla aparecen los valores 0.4495 y
0.4505. Se puede elegir cualquiera de los dos. Por ejemplo
si se elige 0.4505 corresponde a un valor de z
= 1.65 |
|
|
|
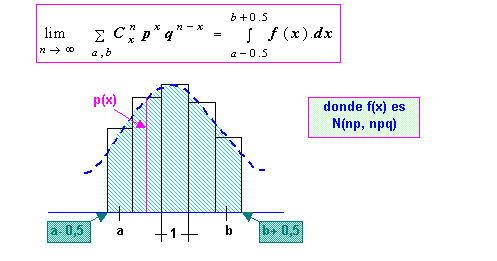
APROXIMACIÓN
A LA NORMAL DE LA DISTRIBUCIÓN BINOMIAL |
En la
práctica la aproximación es buena cuando np y nq son > 15
En tal caso, las probabilidades binomiales estimadas de x
éxitos
se obtienen a partir de
P (x - 0.5< X< x + 0.5) en la distribución normal con media
np y varianza
npq.
| Ejemplo |
Sea una
variable Binomial con n = 40 y p = 0.4, calcular
mediante la aproximación normal la probabilidad de obtener 8
éxitos
|
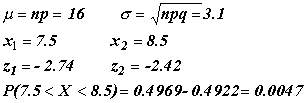
|
Mientras
que la probabilidad exacta calculada por la binomial es P(8) =
0.0040, el error relativo es :
( 0.0047-
0.0040 ) / 0.004 = 0.1750 |
|
|
| Las
distribuciones asociadas a la distribución normal como t,
F ,
Chi cuadrado, se verán a parte con las aplicaciones
da cada una de ellas |
|
Tus
sugerencias - Página principal
-
 Escríbenos
Escríbenos

![]()
![]()


![]()
![]()
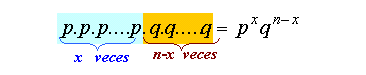
![]()
![]()
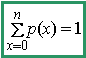

![]()
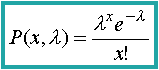

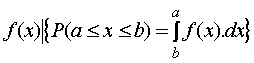
![]() hasta un valor dado de
x
(en la figura: a), o sea la probabilidad de no
superarlo
hasta un valor dado de
x
(en la figura: a), o sea la probabilidad de no
superarlo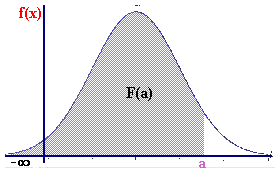
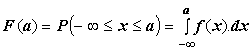
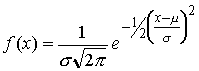
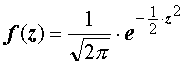
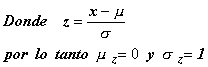


![]()

![]() )
)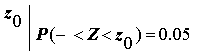
![]() (teorema
de de Moivre)
(teorema
de de Moivre)