

 |
PROBABILIDAD
|
ejercicios
|
|
PRINCIPIOS DE
PROBABILIDAD
|
| Hay muchos
fenómenos reales que se comportan de una manera tan regular que son
absolutamente predecibles (muchas leyes físicas), sin embargo existen
fenómenos (fenómenos aleatorios) en los cuales los resultados no
pueden predecirse con certeza, lo que lleva por lo tanto a un estado de
incertidumbre |
|
Al describir
una experiencia aleatoria es esencial especificar qué aspectos del
resultado nos interesa observar o sea cuál de la descripción es
nuestro criterio para considerar 2 resultados como diferentes. Esto se
logra a partir del espacio muestral |
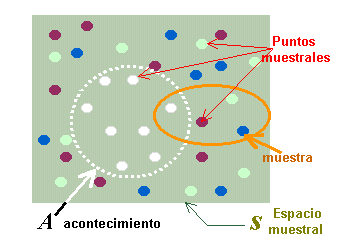 |
Cada
uno de los resultados posibles dentro del espacio muestral (S
)constituye un punto
muestral.
Así en el ejemplo
tendríamos 34 puntos muestrales.
De los cuales 8 son blancos, 9 rojos, 8 azules y 9 verdes.
Cada color, define un resultado posible.
El subconjunto del espacio muestral asociado con ese
resultado y definido por todos los puntos muestrales con el mismo
resultado, se denomina acontecimiento (A)
El subconjunto
del espacio muestral, seleccionado en base a algún criterio con la finalidad
de extraer conclusiones relativas a ese espacio, se denomina muestra |
| Supongamos
que el espacio muestral se compone de un número finito de acontecimientos
A1,
A2.... An
o sea |
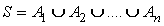 |
y que sean
mutuamente excluyentes entre sí, |
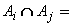 |
f |
|
| Si
suponemos que todos los acontecimientos tienen la misma probabilidad
P (A1)
= P (A2) =.....=P ( An ) |
|
Por lo que
P (Ai
) = P (S) / n =1/ n |
|
| Si tenemos un
acontecimiento A
formado por la unión de m
acontecimientos
Ai |
|
A
= Ai 1 Ai 2
...... Ai n
------
m
veces ---------- |
|
P
(A ) = m
P (Ai
)
= m
P(S) = m
. 1/ n = m
/ n
n |
| En otras
palabras la probabilidad según la definición clásica es el cociente
entre los casos favorables sobre los casos posibles |
| La probabilidad
fue también considerada como resultado de muchos ensayos o pruebas
sin que se pueda pensar en calcularlo de antemano. Es lo que se
llama definición experimental, estadística o frecuencial de la
probabilidad |
|
Interpretación
de la probabilidad
¿Cuál es el
significado de una afirmación tal como P (A) = 0.4?
Se puede dar a P ( A) cualquier interpretación con tal de que ella satisfaga
los axiomas, en tal caso estos números
llamados probabilidades obedecerán todas las leyes de la teoría |
| Interpretación
clásica |
La
definición a priori, fija la probabilidad sin depender de
ninguna experiencia y por lo tanto no está apoyada en ninguna
inferencia inductiva. Constituye un intento de imponer al dominio del azar
(y por lo tanto de la incerteza) un esquema sacado del dominio de la
necesidad. Implica el conocimiento de todo el universo (espacio
muestral) lo que en el mundo de los fenómenos reales es casi imposible
por lo que no constituye una ley universal válida para todas las
clases de hechos
Por otra parte supone que el número de casos favorables y el de casos
posibles es finito, en este caso la probabilidad de un suceso es siempre
un número real comprendido entre 0 y 1 . Pero si hay infinitos casos
posibles, la definición plantea el problema de la división por infinito |
| Interpretación
frecuentista |
Para
que un experimento sea llamado aleatorio se requiere que él sea
indefinidamente repetible, al menos teóricamente
De acuerdo con este concepto p.ej.: un experimento que consista en visitar
mañana a las 12:00 un lugar determinado y observar si llueve o no, ya que
hoy es imposible saber lo que pasará mañana a esa hora.¿será un
experimento aleatorio con dos resultados posibles? NO!
Los frecuentistas considerarán esta experiencia sólo como un punto
muestral en un espacio muestral de n
repeticiones y f
es el número de
aquellas en que ocurrió el acontecimiento A
.
Un teorema matemáticamente demostrable dice que la diferencia entre fr
y P cuando
n
tiende a infinito, tiende a cero (ley de los grandes
números) |
Quiere
decir que para cualquier número positivo, tan pequeño como se quiera,
existe un valor de n suficientemente grande para asegurar la desigualdad :
| fr -
P | < e
Se podría
entonces repetir el experimento un número suficientemente grande de
veces de modo que la frecuencia relativa difiera muy poco de P, tendiendo
a ser igual
Es, además, un hecho experimentalmente observable que a medida que n
crece la frecuencia relativa fr de un suceso A tiende
a estabilizarse alrededor de cierto valor límite. Este valor límite
es por definición la probabilidad de A
Sin embargo, la definición en la práctica tiene una dificultad
insuperable, que es que aunque n aumente, existe la posibilidad de
que la diferencia entre la frecuencia relativa observada y la probabilidad
teórica aumenta en lugar de disminuir
Por
ejemplo:
Se lanza 216 veces un dado donde se obtiene 36 veces un 6, la
probabilidad teórica de sacar un 6 =1/6 la fr en esta experiencia=
36/216 =1/6 por lo cual
fr -P = 0
Pero si el dado se lanza ahora 600 veces y se obtiene 105 veces
el 6; fr = 105/600 y la diferencia
fr - P = 105/600 - 1/6 = 0.0083
Aquí la fr se
apartó de la esperada, este tipo de discrepancias siempre van a
existir con respecto a la fr con respecto al valor "
verdadero"
|
 |
| En la
figura se observa como a medida que el nº de ensayos en una
experiencia dada la fr tiende a estabilizarse en un
valor P teórico. Pero también se ve que por esa misma
fluctuación en un nº determinado de ensayos
(a) la fr
coincide con P, pero en un nº mayor de ensayos (b)
la fr se aparta de ese valor "verdadero" |
|
| Se llama
probabilidad P, definida en todos los acontecimientos posibles y
mutuamente excluyentes, dentro de un espacio muestral, a un número real
que cumple los siguientes axiomas: |
| 1 |
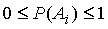
|
para todo A i |
| 2 |
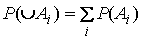
|
siendo los
distintos A i incompatibles |
| 3 |
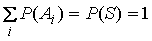
|
siendo S el
espacio muestral |
Si el espacio
muestral es finito o infinito numerable el espacio de probabilidad
se llama discreto.
Un caso particular se da cuando los acontecimientos tienen la misma
probabilidad, en este caso el espacio muestral es equiprobable.
Cuando el espacio muestral es infinito no numerable, se dice que es
continuo |
| Sea B un
acontecimiento y A1, A2, A3...An
una serie de acontecimientos disjuntos tales que la ocurrencia
de B vaya necesariamente acompañada de la ocurrencia de ellos es: |
Sea un
acontecimiento B y una serie de acontecimientos disjuntos An
tales que la ocurrencia de B va necesariamente acompañada de
la ocurrencia de uno de ellos.
Si se conocen las
probabilidades A i, y las probabilidades condicionales B tal
que A i. Siendo que ocurrió B
¿Cuál es la
probabilidad de cada A i dado? |
|
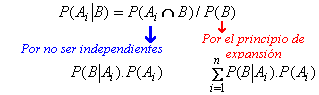 |
|
| La
ley de los grandes números se demuestra a partir del teorema
de Tchebychev y
se puede interpretar como que, a medida que aumenta el tamaño de muestra,
aumenta la probabilidad de obtener mejores estimaciones a partir de
una muestra |
| forma
fuerte |
forma
débil |
|
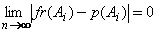
|
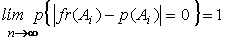
|
|
estando
p(A i) (para ambas formas) definida como: |
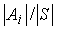 |
(definición
clásica) |
|
En
un cruzamiento de tipo Aa x Aa se obtienen 3 descendientes.
| 1.-
La probabilidad de que sean todos Aa es: |
a)
0.5 + 0.5 + 0.5
|
 |
|
b)
0.5 3
|
|
c)
3 x 0.25
|
| 2.-La
probabilidad de que sean 2 de tipo Aa y 1 de tipo aa es: |
a)
0.5+ 0.5 + 0.25
|
 |
|
b)
2 x 0.5 + 0.25
|
|
c)
0.5 2 x 0.25
|
|
La
probabilidad de contraer hepatitis con una unidad de sangre es de 0.01
(1%). Un paciente recibe 2 unidades de sangre durante su estadía en el
hospital.
| La
probabilidad de que NO contraiga hepatitis como consecuencia de la
transfusión es: |
|
a)
0.012
|
 |
|
b)
0.992
|
|
c)1
- 0.992
|
|
|
| Sean
dos sucesos A y B pertenecientes a un mismo espacio muestral. Si A y B son
independientes cuál de las afirmaciones es correcta:
|
Tus
sugerencias - Página principal
-
 Escríbenos
Escríbenos
![]()
![]()

![]()
![]()
![]()
![]()
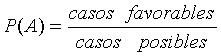
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
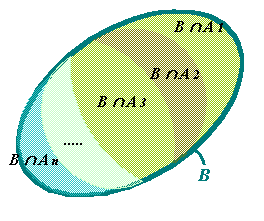
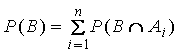
![]()
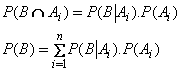
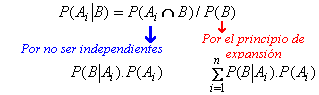
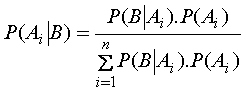
![]()
![]()
![]()

![]()
![]()
![]()
![]()