|
DISTRIBUCIÓN DE POISSON |
| Supongamos
un soporte continuo (p.ej. tiempo o espacio) dividido en n intervalos
sin puntos en común y un acontecimiento que tiene la misma
probabilidad p
de ocurrir en cualquiera de estos intervalos Cada intervalo puede ser considerado como un ensayo independiente y la probabilidad de obtener x éxitos en los |
|
| n ensayos tendrá distribución binomial . | 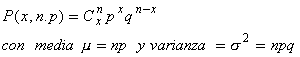 |
| Si se considera que la probabilidad de ocurrencia de un éxito en un intervalo dado depende solamente de la longitud del intervalo, el producto l = np es constante. Al aumentar n, p disminuirá proporcionalmente p = l / n |
| Haciendo tender
n
a infinito, p
tenderá a cero, manteniéndose l
constante, finita y distinta de cero La distribución resultante será entonces: |
|
|
| En
la expresión anterior, los nx
se cancelan, el producto (1)(1
- 1/n)....(1 - ( x-1)/n)
tiende a 1, el factor (1 - l / n)n |
||
| tiende a e-l , (1 - l / n)x tiende a 1 y por lo tanto: | 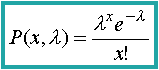 |
con
media m
=np
= l con varianza s 2 = npq = l (si p tiende a 0, q tiende a 1) |