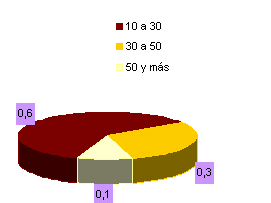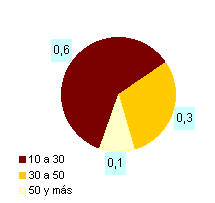Spanish Banner: Intercambio de Enlaces.

| ¿Para qué
graficamos? |
1º |
Con una simple
mirada , nos damos cuenta del desarrollo del fenómeno |
| 2º |
Sirven
para controlar las variaciones de los datos recogidos |
| 3º |
Algunas veces
sugieren la necesidad de investigaciones nuevas |
| 4º |
Facilitan el
descubrimiento de relaciones entre los fenómenos (utilidad heurística) |
| Existen
muchos tipos de gráficos, de acuerdo a los datos, lo que queremos
representar y para qué.
Hoy en dia, planillas
electrónicas como Excel o programas de estadística traen múltiples opciones para realizar
gráficos de gran calidad, por lo que aquí
mostramos los tipos básicos de gráficos, que tiene utilidad
estadística |
|
|
| Diagramas
de tallo y hojas (Diagrama de Tuckey) Un
procedimiento semigráfico para variables cuantitativas, es útil
especialmente si el
número de datos es pequeño.
Procedimiento
1.-
Se redondean los datos a dos o tres cifras significativas,
expresándolos en unidades convenientes
|
2.-
Se disponen en una tabla con dos columnas separadas por una línea
vertical:
- Para datos con 2
dígitos se escriben a la izquierda de una línea los dígitos de las
decenas (que forman el tallo) y a la derecha las unidades, que serán
las hojas: por ejemplo: 65 se escribirá 6 | 5
- Para datos de 3 dígitos
el tallo estará formado por los dígitos de las centenas y de las
decenas, que se escribirán a la izquierda, separados de las unidadaes.
Por ejemplo: 265 se escribe 26 | 5
3.-
Cada tallo define una clase, y se escribe una sola vez . El número
de hojas representa la frecuencia de dicha clase |
| Ejemplo:
Datos
recogidos |
11.357 |
12.542 |
11.384 |
12.431 |
14.212 |
15.213 |
13.300 |
11.300 |
|
17.202 |
12.710 |
13.455 |
16.143 |
12.162 |
12.721 |
13.420 |
14.698 |
|
|
Datos redondeados |
11.4 |
12.5 |
11.4 |
12.4 |
14.2 |
15.2 |
13.3 |
11.3 |
|
17.2 |
12.7 |
13.5 |
16.1 |
12.2 |
12.7 |
13.4 |
14.7 |
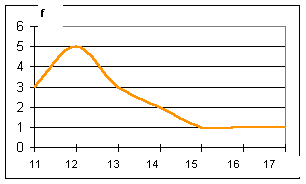
| Diagrama
de tallo y hojas |
frecuencia |
 |
|
11 |
3, 4, 4 |
3 |
| 12 |
5,
4, 7, 2, 2 |
5 |
| 13 |
2,
5, 4 |
3 |
| 14 |
2,
7 |
2 |
| 15 |
2 |
1 |
| 16 |
1 |
1 |
| 17 |
2 |
1 |
|
El diagrama de
tallo y hojas permite visualizar de una forma rápida , la forma
(como se ve en el gráfico de arriba) de la distribución de frecuencias
de la variable que se está estudiando |
|
Gráficos
para variables discretas
|
|
En las variables discretas entre 2 valores consecutivos no
existe ningún valor intermedio , por lo que la frecuencia
simple de cada valor estará dada sólo por la altura de una línea
perpendicular a las abscisas (valor de x), el ancho de esa línea no tiene
ningún significado , sólo el estético.
|
| El
diagrama así obtenido para frecuencias simples (absolutas o relativas )se
llama diagrama de
bastones o espectro |
El
diagrama para frecuencias acumuladas (absolutas o relativas ) se
llama diagrama en
escalera |
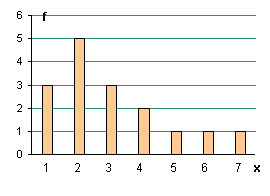 |
 |
| Gráficos
para variables continuas |
En
las variables continuas la posibilidad de que la variable pueda asumir cualquier
valor hace
que el tipo de gráfico
|
| sea diferente que para el caso
anterior. El gráfico más utilizado
es el HISTOGRAMA. |
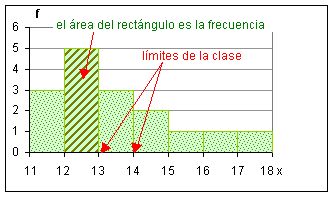
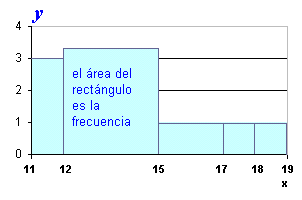
| Cada
clase está representada por un rectángulo cuya base es la extensión
del intervalo de clase y su área la frecuencia. |
| Es
importante destacar que la frecuencia está representada
por el área del rectángulo, así en gráficos donde todas las
clases tienen la misma extensión se puede representar directamente la
frecuencia en ordenadas ya que es proporcional al área
CUIDADO! Si
los intervalos son de diferente extensión, NO se puede
poner directamente la frecuencia en ordenadas y se debe utilizar la densidad
de frecuencias ( y ) |
| densidad
de frecuencia ( y ) = frecuencia relativa / extensión del intervalo |
| histograma
de intervalos de clase con la misma extensión |
histograma
de intervalos de clase de extensión diferente |
 |
 |
| En
un par de ejes cartesianos , se marca en abscisas el punto
medio o marca de clase |
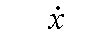 |
| para cada
categoría de la variable y en ordenadas la frecuencia que
corresponde a cada clase.
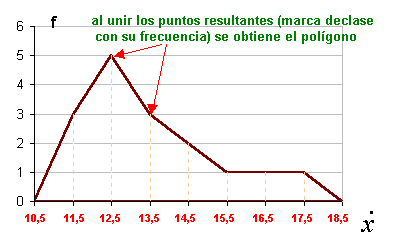
Se unene los puntos
resultantes, al cerrar el gráfico en los extremos con frecuencia 0,
se obtiene el polígono de frecuencias simples ( absolutas o relativas) |
| x |
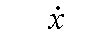 |
f |
poligono
de frecuencias simples absolutas |
| 10
- 11 |
10,5 |
0 |
 |
| 11
- 12 |
11,5 |
3 |
| 12
- 13 |
12,5 |
5 |
| 13
- 14 |
13,5 |
3 |
| 14
- 15 |
14,5 |
2 |
| 15
- 16 |
15,5 |
1 |
| 16
- 17 |
16,5 |
1 |
| 17
- 18 |
17,5 |
1 |
| 18
- 19 |
18.5 |
0 |
| En
el límite, cuando el número de intervalos tiende a infinito , la
amplitud de cada intervalo tiende a 0 , el histograma y el polígono de
frecuencias tiende a confundirse y a adoptar la forma de una curva lisa en
la mayoría de los casos |
| |
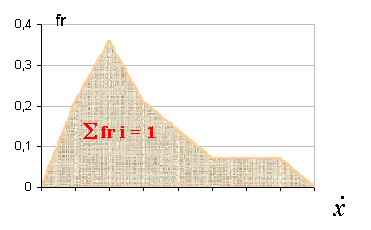 |
| La
frecuencia relativa total (área total) es la suma de las frecuencias
relativas simples (fr) debajo de la curva y vale 1 |
| |
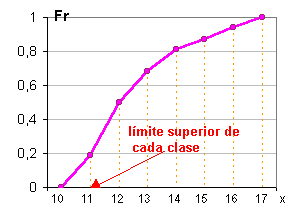
| Si
interesase saber cuantos casos hay por debajo de
e incluso hasta un valor x determinado, se trabaja con frecuencias
acumuladas (F) |
 |
|
| Para
graficar el polígono de frecuencias acumuladas, en abscisas
se marca el límite superior de cada clase y en ordenadas la
frecuencia acumulada relativa (Fr, Fr%) de la clase correspondiente |
|
|
| Cuando la
variable que estamos estudiando es de tipo categórica, una
representación gráfica adecuada es el DIAGRAMA
DE BARRAS
En este tipo de diagrama
las categorías se representan como barras donde el largo es la
frecuencia y el ancho no tiene relevancia estadística |
| Nº
de variables |
tipo |
observaciones |
| 1 |
barras
simples verticales |
los
niveles de la variable categórica se pone en el eje de las abscisas |
| barras
simples horizontales |
es
útil cuando las categorías asumen nombres largos, entonces las
categorías pasan al eje de ordenadas y la frecuencia al de abscisas |
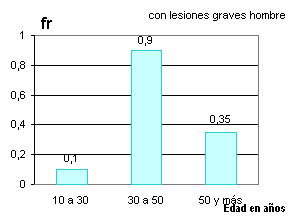
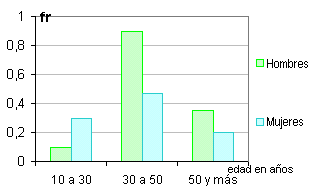
| 2
o más |
barras
combinadas verticales |
una
de las variables categóricas aparece en el eje de abscisas (por ejemplo
como en el gráfico, edad ), la otra variable (sexo) está dada por los
pares de barras pegados, cada barra identificada con un color para
cada sexo |
| barras
combinadas horizontales |
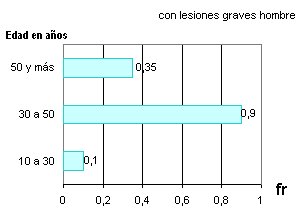
es
una forma de diagrama útil, cuando tenemos 3 variables, por
ejemplo: se quiere tener una idea de la distribución de lesiones graves y
lesiones leves , según sexo y según edad |
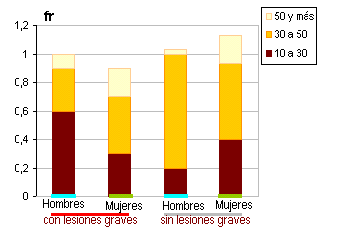
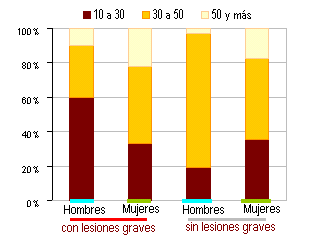
| barras
compuestas |
Estas
son útiles cuando cada categoría puede ser subdividida según una
característicasecundaria.
Se puede representar
de dos maneras según como se contabilicen las proporciones de las
subcategorías |
 |
 |
 |
 |
 |
 |
|
DIAGRAMA
DE SECTORES Otra
forma, es representar porcentajes de las categorías en el total de las
observaciones |
 |
|
| El
círculo representa el total de una característica, se divide en sectores
cuyo ángulo refleja el porcentaje del total para cada categoría. Como el
círculo tiene 360º éstos representan el 100% de las observaciones, el
ángulo correspondiente de cada categoría se calcula facilmente. |
| Edad
(en años) |
fr% |
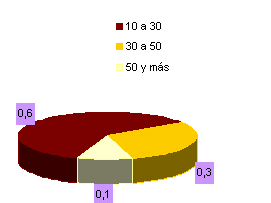 |
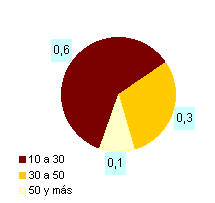 |
| 10
- 30 |
0.6 |
| 30
- 50 |
0.3 |
| 50
y más |
0.1 |
|
| Cuando lo que
interesa es la relación que existe entre dos variables continuas,
el gráfico más sencillo es el que en un par de ejes se representan los
valores de cada una de las variables, y para cada valor que asuma una,
habrá algún valor de la otra. |
| A
la inspección, muchas veces los diagramas de dispersión dejan al
descubierto una relación funcional de las variables.
De esta forma se pueden
ajustar modelos de regresión a los datos observados (si lo que se busca
es predecir) o calcular correlaciones (si lo que interesa es solamente la
asociación de las variables) |
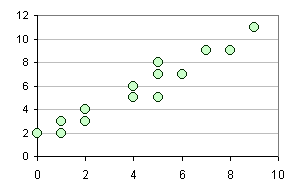 |
| Como
se ve en el diagrama de la derecha, se puede descubrir una relación
lineal entre ambas variables. No siempre la relación
tiene que ser de tipo lineal, pueden ser curvilíneas, esto se puede ver
más detalladamente en distribuciones bivariadas, regresión y
correlación |
| ejercicios |
Para responder,
cliquear sobre la respuesta que considere correcta (debe disponer de
Explorer 5 para que funcione correctamente)
|
solución
|
| 1.-
Al representar las frecuencias en un diagrama de sectores, si la
frecuencia vale 20 y el tamaño de muestra es 120, entonces el sector
medirá:
|
|
a.-
30º
|
|
b.-
80º
|
|
c.-10º
|
|
d.-60º
|
|
|
|
|
|
|
|
|
|
| 2.-Una
variable discreta puede ser representada graficamente con un histograma
|
a
|
Sí,
es la forma habitual de representar ese tipo de variable
|
|
b
|
No,
se representa por diagrama de barras
|
|
c
|
Sólo
en algunos casos, cuando asume pocos valores
|
|
d
|
Sí,
si se realiza una corrección por continuidad
|
| 3.-Si
se quiere comparar graficamente 2 distribuciones de frecuencias de
variables numéricas, el tipo de gráfico más adecuado es
|
a
|
Polígono
de frecuencias acumuladas simples
|
|
b
|
Polígono
de frecuencias absolutas simples
|
|
c
|
Polígono
de frecuencias relativas simples
|
|
d
|
Histograma
de frecuencias relativas
|
Tus
sugerencias - Página principal
-
 Escríbenos
Escríbenos
![]()
![]()




![]()
![]()