TEST NO PARAMËTRICOS
Al plantear hipótesis
relativas a medias poblacionales, éstas pueden ser bicaudales
(hipótesis de que la media poblacional sea igual a un valor dado)
o unicaudales ( hipótesis de que la media poblacional sea mayor/igual
o menor/igual a un valor dado) La hipótesis
nula (Ho)
puede testarse teniendo en cuenta la distribución de las medias en
el muestreo Entonces
si la probabilidad de obtener una media tanto o más alejada
de k
es baja,
se rechaza la
hipótesis nula Como la distribución de
las medias es normal con media
m
(por hipótesis igual a k)
y desviación
típica La comparación que
se hace es : LCi =
LCs =
e Es posible demostrar que
ese cociente sigue una distribución
de Student con n-1
grados de libertad La distribución de t presenta
una forma parecida a la normal, con media 0 y desviación
típica
t = 2.78 Estimación de m Tus
sugerencias - Página principal
- 
INFERENCIA:
UNA MUESTRA
ejercicios
resueltos
TEMAS
RELACIONADOS
CONTENIDO
APLICACIONES DE LA DISTRIBUCIÓN NORMAL
test
bicaudales , test
unicaudales
APLICACIONES DE LA
DISTRIBUCIÓN DE t
(student)
APLICACIONES
DE LA DISTRIBUCIÓN NORMAL
Verificación
de hipótesis relativas a
medias con
s conocida
test
bicaudales
Si se
plantea la hipótesis de que la media poblacional es igual a un
valor dado
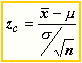
El
valor de z calculado es el estadístico z
Si la
probabilidad de obtener un valor (absoluto) de
z calculado mayor
que el valor de z
hallado en la tabla
de la distribución normal, es menor que a
/ 2 se
rechaza la
hipótesis nula, en caso contrario se acepta
En
la práctica, primero se halla en la tabla el valor de z que deja
por encima de él un a
/ 2
. Este valor se llama
valor crítico de z
test
unicaudales
Si la Ho fuese
del tipo :
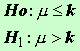
El
área de rechazo se encuentra de un sólo lado de la curva.
El test se realiza en igual forma que en el caso bicaudal, pero los
valores críticos son diferentes: se busca en la tabla el valor de z
que deja por encima de él el nivel de significación a
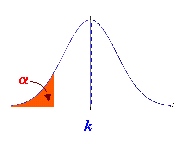
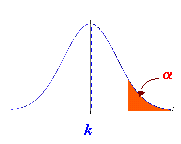
Si
Ho : m
k
. El valor crítico es el z tabulado que deja por encima, de él a.
Se rechaza Ho
cuando z calculado > z tabuladoHo
: m
k
. El valor crítico es el z tabulado que deja por debajo, de
él a.
Se rechaza Ho
cuando z calculado < z tabulado
Estimación
de medias con s
conocida
Cuando se
observó una media muestral
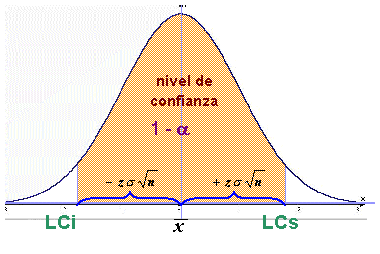
y se desea hacer una estimación por intervalo
a nivel de confianza
1- a,
se procede en forma
similar a la verificación de hipótesis bicaudal
Se busca en la tabla el valor crítico de z que deja por encima de
él a /
2 y después se calcula
los límites de confianza
Aunque
la expresión es formalmente incorrecta, es habitualmente aceptado
escribir el resultado
como :
LCi
m
LCs
TAMAÑO
DE MUESTRA PARA ESTIMAR MEDIAS
Si se desea
saber el tamaño de muestra necesario para estimar una media poblacional
con un error menor que un valor e,
basta tener en cuenta que el máximo desvío es
a 
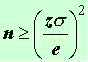
Verificación
de hipótesis relativas a proporciones
muestras
grandes
De la misma
forma que para las medias se pueden plantear tres tipos de hipótesis
nulas. La proporción
poblacional es igual a un valor dado, que es menor/igual o mayor/igual
El valor
de z calculado
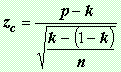
El resto
del procedimiento es igual que el visto para las medias
Estimación
de proporciones
muestras grandes
Como no se
dispone de un valor de P,
se utiliza para calcular el error típico, el valor observado p.
Siendo z el valor crítico (tabulado)
Los límites de
confianza inferior y superior del intervalo se calculan:
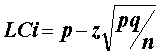
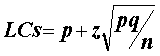
TAMAÑO
DE MUESTRA PARA ESTIMAR PROPORCIONES
El tamaño de
muestra necesario para estimar una proporción poblacional se calcula
como:
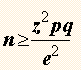
Ejercicios
resueltos de aplicaciones de la distribución Normal
-
Estimación de medias
- Verificación de hipótesis
relativa a medias
- Tamaño de muestra-Estimación
de proporciones
-Verificación de hipótesis
relativa a proporciones
-Tamaño de muestra
DISTRIBUCIÓN
DE t
Como se vio
anteriormente, el cociente
tiene distribución
N(0,1)
En la mayoría
de las situaciones reales, el valor s
es desconocido,
debiendo estudiarse a partir
del estadístico :
El cociente
NO tiene
distribución normal sino distribución de t.
La desviación
poblacional está estimada a través de la desviación muestral. Hay
que recordar que s
es un parámetro y que es
una variable aleatoria que depende de la muestra.
El
número de grados de libertad (n)
es en general igual al tamaño de la muestra (n) menos el número de
parámetros estimados previamente.
Como para
estimar la varianza (y la desviación típica) es necesario calcular
antes la media, el número de grados de libertad es en este caso
n-1
siendo n
los grados de libertad
Distribución
de t con 1 grado de libertad, al hacer "clic" en la imagen
se puede ver la distribución con 120 gl
TABLA
DE t
En
esta tabla de t las áreas se acumulan desde menos infinito hasta un
valor de t.
En la 1a columna, se encuentran los grados de libertad, en el cabezal las
áreas y en el cuerpo de la tabla los valores de t.
Ejemplo
: ¿Cuál es el valor de t , para 4 grados de libertad, tal
que deja un 95% central?
Estimación
y verificación de hipótesis relativas a medias
Se
procede igual que con s
conocida, sustituyendo la distribución normal por la de t
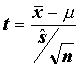
Verificación de Ho:
= k
Para una muestra de tamaño n, con 
y
(desviación típica centrada )
