"La
imaginación, impaciente por remontarse a las causas, se complace en
crear hipótesis y a menudo deforma los hechos para plegarlos a su
labor: en tales casos, las hipótesis son peligrosas. Pero cuando
sólo se las considera como medios para conectar entre sí los
fenómenos a fin de descubrir sus leyes, cuando, procurando no
atribuirles realidad, se las rectifica continuamente con ayuda de
nuevas observaciones, entonces pueden llevarnos a las causas
verdaderas o, por lo menos, ponernos en condiciones de inferir de
los fenómenos observados aquellos que, dadas las circunstancias,
han debido originarlos"
Pierre Simon de Laplace Los estadísticos son
funciones de los valores observados en la muestra. (ya se han visto
algunos, como la media, la desviación típica, percentiles) La verificación
de hipótesis
es el proceso que lleva a juzgar la credibilidad de afirmaciones (hipótesis)
relativas a las
poblaciones (habitualmente
a sus parámetros)
de las que fueron extraídas las muestras Ho
cierta Ho
falsa rechazar Error
I Decisión No
rechazar Error
I DEFINIR
LA HIPOTESIS A CONTRASTAR La
estimación
es el proceso
y el resultado
de inferir un valor o un intervalo de valores para un parámetro
poblacional a partir de una muestra Tus
sugerencias - Página principal
- 
INTRODUCCIÓN
A LA INFERENCIA ESTADISTICA
TEMAS
RELACIONADOS
CONTENIDO
Ensayo filosófico sobre las probabilidades
(de las diversas formas de acercarse a la certeza) 1795
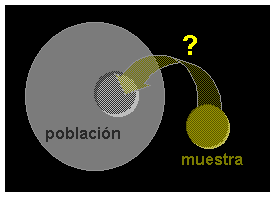
La
inferencia estadística es el proceso a través del cual se
extraen conclusiones relativas a una
población a partir
de una muestra . La expresión inferencia se utiliza también
para designar su resultado y la rama de la estadística que se ocupa
de ella
Se
basa en el uso de estadísticos cuya distribución en el muestreo se
conoce
Por ser funciones de una variable aleatoria, los
estadísticos son también variables
aleatorias y
por lo tanto a cada uno de ellos se le puede asociar una
distribución de probabilidad llamada distribución
en el muestreo
del estadístico dado.
Es
posible pasar de la Teoría de la Probabilidad a la Inferencia
Estadística
En la
mayor parte de las técnicas que se describen aquí, las inferencias
(conclusiones) se refieren a parámetros poblacionales. Sin
embargo, es posible realizar inferencias que no se relacionen con
parámetros (ver análisis de frecuencias).
Según
la finalidad de la Inferencia
Estadística se
puede dividir en :
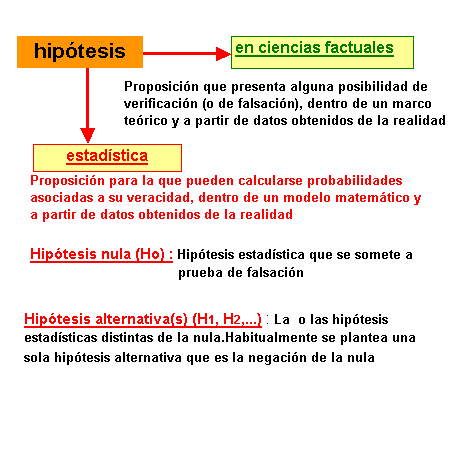
TEORÍA
DE LA VERIFICACIÓN DE HIPÓTESIS
Es interesante
tener en cuenta que la veracidad de una hipótesis no
puede ser probada nunca
Lo que se puede hacer es afirmar que tiene tal o cual probabilidad
de ser falsa
Si esa probabilidad es muy alta (95% o 99%) por ejemplo, se concluye
que la hipótesis es poco creíble y se califica provisoriamente
como falsa. Si no se consigue "falsar" (rechazar) la
hipótesis, se acepta provisionalmente como verdadera.
Esta calidad de provisorias de las conclusiones estadísticas no
debería sorprender a nadie: toda
la ciencia es un constructo provisorio
Ejemplificando
La
Hipótesis nula puede ser : un parámetro q
que tiene un valor k y
la Hipótesis alternativa
será su negación
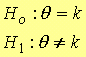
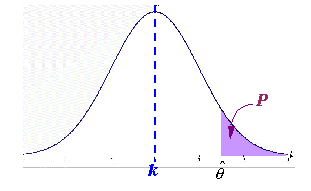
Si se toma
una muestra y en ella se calcula un estadístico
cuya
distribución en
el
muestreo
en el caso de que Ho sea verdadera se conoce, se puede determinar
qué
probabilidad
(P)
hay de que si el verdadero valor del parámetro es k
se obtenga un valor observado
del estadístico
, tan alejado ( o más) de k
.
Si
P
es muy baja la probabilidad de que la muestra no
pertenezca a una población con q
= k
es muy alta , por lo tanto se rechaza Ho. Consecuentemente
se acepta H1
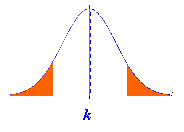
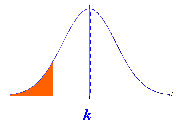
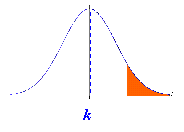
Los
tests ( o pruebas) asociados con las hipótesis pueden ser uni o bi
caudales, según las hipótesis planteadas
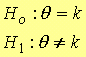
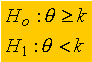
TIPOS
DE ERRORES
Se pueden
cometer dos tipos de errores en la verificación de hipótesis
ERROR
TIPO I :
RECHAZAR LA Ho SIENDO CIERTA
El
hecho de que P
sea muy bajo no califica el acontecimiento como imposible.
Simplemente que tiene poca
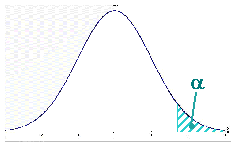
probabilidad
de ocurrir al azar.
A la
probabilidad de cometer error tipo I se la denomina nivel
de significación a
Habitualmente
el investigador fija a priori el nivel de significación
crítico para rechazar Ho ( a)
. Si P
es menor
que a
, se rechaza. En caso contrario, se acepta Ho
Críticas
a la elección del nivel de significación
Se
pueden puntualizar 3 críticas principales:
1.-
El resultado depende de a
que es arbitrario. Se puede entonces utilizar en su lugar, el
nivel critico del test p,
o sea, la probabilidad de obtener una discrepancia mayor o
igual a la observada en la muestra cuando Ho es cierta
Por
lo tanto p
no se fija a priori sino que se fija a partir de la muestra
2.-
Dar sólo el resultado del test no permite diferenciar el
grado de evidencia que la muestra indica a favor o en
contra de la Ho, es decir que hay que especificar con que
probabilidad d1 o d2 se
rechazan, porque eso indica el grado de evidencia
3.-
Si la Ho especifica un valor de un parámetro y el test
conduce a rechazarlo sería conveniente indicar cual es la
estimación más plausible del parámetro
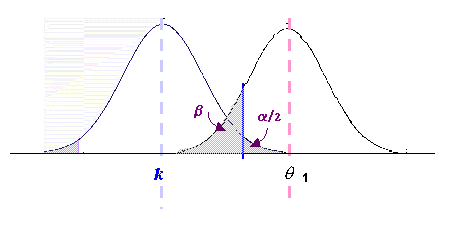
ERROR
TIPO II :
ACEPTAR LA Ho SIENDO FALSA
En
realidad, q
puede asumir infinitos valores distintos de k
. Si el verdadero valor de q
no dista excesivamente del postulado en Ho, es posible aceptar ésta
siendo falsa:
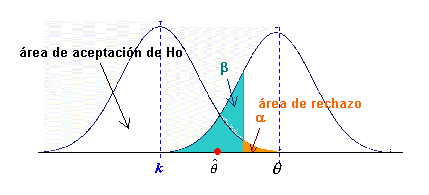
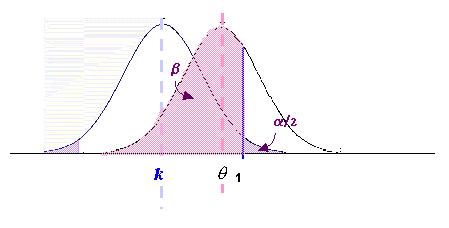
Como el
valor observado
cae en el área de aceptación de Ho, no se rechaza la hipótesis.
Sin embargo el valor verdadero del parámetro q
es distinto
de k
. La
probabilidad de cometer un error de tipo II es b.
Al valor (1-b)
se le llama potencia
de un test.
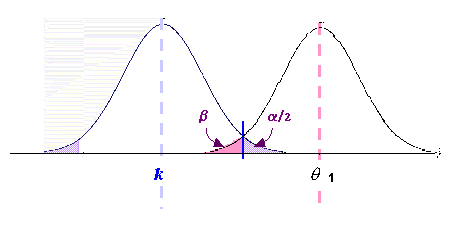
El valor b
depende de a
y del valor alternativo que se ponga para q.
Cuanto
menor sea a
, mayor será b
.La única forma de disminuir ambos errores, es aumentar el tamaño
de la muestra (n).
Ho
a
nivel de significación
correcta
1-b
potencia
Ho
Decisión
correcta
b
ELEMENTOS
DE LA PRUEBA DE HIPÓTESIS
1
Por
ejemplo Ho:q
= q
o
¿Cómo plantear las hipótesis?
2
PRUEBA
ESTADISTICA ( o medida de discrepancia) A EMPLEAR
Definir
una medida de discrepancia entre la muestra y la Ho del tipo d
(q
; q
o) con una distribución conocida.
¿Cómo elegir la prueba a utilizar?
3
NIVEL
DE SIGNIFICACIÓN; VALORES CRÍTICOS
Significa,
fijar una regla para determinar si la discrepancia es
suficientemente grande como para ser incompatible con Ho (lo
más simple es fijar a
, lo que determina un valor crítico o
tabulado d t )
¿Qué se debe tener en cuenta al
elegir a?
4
CONTROLAR
LOS SUPUESTOS
De
acuerdo a la prueba o medida de discrepancia, se deben cumplir
ciertos supuesto como normalidad, independencia, etc. Éstos
deben controlarse para poder aplicar la prueba.
Hay que tener en cuenta que la prueba estadística (o
medida de discrepancia) por sí misma NO sirve para
identificar el o los supuestos erróneos
¿Cómo controlar los supuestos?
5
EXPERIMENTO
Y CALCULO (de la prueba estadïstica)
Tomar
la muestra, estimar q
, calcular la
discrepancia
dc (q
; q
o)
6
COMPARACIÓN
( valores calculados con los críticos)
La
comparación de ambos valores calculados (dc
)y critico (d
t )
guía hacia la decisión a tomar
7
DECISIÓN
y CONCLUSIONES
Si
: dc
> d
t se rechaza la Ho
Si : dc
< d
t NO se rechaza la Ho
Al rechazar la Ho se acepta implícitamente que la Ho es
falsa, lo que implica la elección de otra hipótesis H1
TEORÍA
DE LA ESTIMACIÓN
En
algunas ocasiones lo que se desea es estimar el valor de un
parámetro
La
estimación puede ser hecha:
por punto
En este caso se da un
solo valor supuesto
o
por intervalo
En
este caso se dan dos
valores límites
que dejan un intervalo al cual se supone pertenece el verdadero
valor
La estimación
por punto aunque muy exacta, puede ser muy poco precisa, es decir
tener un margen de error grande, lo que indica su poca fiabilidad, por lo
que es preferible estimar parámetros por medio de
intervalos
cuya precisión es mayor
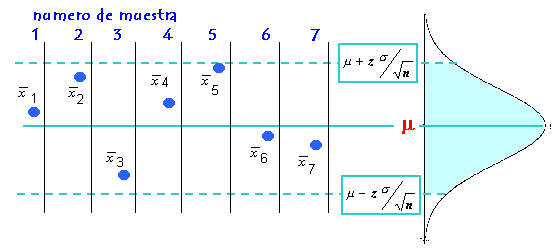
De 100 muestras
que se tomen, sólo 5 (si el nivel de confianza es de 95% ) caerán fuera
del intervalo.
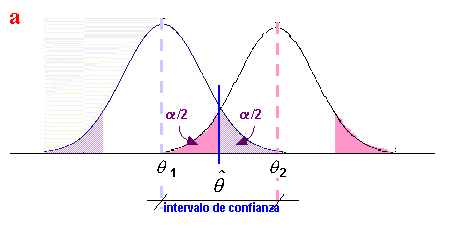
La estimación
por intervalo se basa en el siguiente razonamiento:
¿Cuáles son los extremos q
1, q
2 (límites de
confianza) para el parámetro q
, que son
compatibles a nivel de significación a
con la hipótesis
Ho: q
= siendo
la
estimación?
El resultado en
la práctica es el mismo que se obtendría si suponiendo que
fuese igual al verdadero valor
de q
, se calculase el
intervalo al cual pertenecería la proporción ( 1-
a)
de las estimaciones
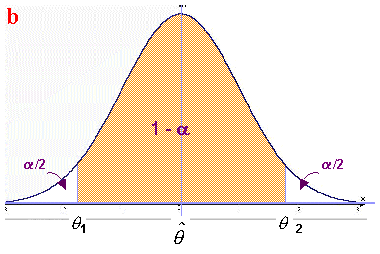
Al
interpretarse un intervalo de confianza generalmente, se tiende a decir:
"hay un 95% de confianza de que el intervalo contenga al
parámetro" o peor " la probabilidad de que el parámetro caiga
dentro del intervalo es del 95%".
Debe tenerse en
cuenta que si bien los límites de confianza q
1, q
2 son los mismos de los casos expuestos más arriba (figs.
a
y
b
), el nivel de
confianza (1-
a)
NO puede considerarse como la probabilidad de que el
verdadero valor de q
pertenezca al intervalo
q
1q
2
