De donde p
= x / n = S w / n es
una media ( TIPO CARACTERISTICAS OBSERVACIONES TEOREMA CENTRAL
DEL LIMITE (o TEOREMA DEL LIMITE CENTRAL) Tus
sugerencias - Página principal
- 
TEORIA
DE MUESTREO (BASICA)
TEMAS
RELACIONADOS
CONTENIDO
Para poder
realizar inferencias estadísticas respecto a un parámetro poblacional a
partir de uno o más estadísticos muestrales, es necesario conocer la
distribución de probabilidad de cada uno de estos últimos considerados
como variables aleatorias, es decir conocer
el tipo de dicha distribución (normal, t, etc) y sus parámetros
NOTA: A
efectos de evitar confusiones en el desarrollo del tema utilizamos,
cuando sea conveniente, la siguiente notación
E(q
) =
Esperanza de una variable cualquiera, q
. Es la media poblacional de q
V (q
) =
Varianza poblacional de q
DISTRIBUCIÓN
MUESTRAL DE LAS MEDIAS
Una muestra
aleatoria de n observaciones independientes de una variable x puede ser
considerada como una colección de observaciones unitarias de n variables
independientes (x1, x2,
....xn
) todas con la misma distribución de probabilidad
CARACTERISTICAS
1
La
suma de esas n
variables ( S
x
) tenderá a distribuirse normalmente cuando n
tiende a infinito (teorema central del
límite) sea cual sea la distribución original de las x
Recordando
que 
,entonces las
medias muestrales tendrán también distribución asintóticamente
normal
2
La
esperanza de la suma (E
(S
x
)) es igual a la suma de las esperanzas (S
( E(
x
)) . Como
todas las x
tienen la
misma esperanza ( media = m),
tenemos:
y, como ,
entonces 
3
Por
ser las x independientes,
la varianza de la suma ( V (S
x))
es igual a la suma de las varianzas
(S
( V(
x
)) .Todas
las x tienen
la misma varianza (s
2),
entonces
por
lo tanto:
CONCLUSION
Las
medias muestrales tienden a distribuirse normalmente con media
(
) igual
a
m
( la
media poblacional de x
)
y varianza (
) igual a 
, siendo s
2
la varianza poblacional de x
Nota
: La convergencia es muy rápida si
x tiene distribución
normal o al menos simétrica. En otros casos se requiere que n
sea mayor o igual a
30
DISTRIBUCIÓN
MUESTRAL DE LAS
PROPORCIONES
El
número de éxitos (x)
en un experimento binomial, puede interpretarse como la suma de los
valores de una variable (w),
tal que w=1 si
la observación es un éxito y w
=0 si es un fracaso
)
CARACTERISTICAS:
La distribución de p
cumplirá las mismas condiciones que la de las medias muestrales
1
Asintóticamente normal
2
E ( p
) = P (proporción
poblacional)
3
Cualquiera
de las siguientes condiciones aseguran una aceptable aproximación a la
normalidad
l n
p > 15 , n q >15
l n
p q > 5
l
DISTRIBUCIÓN
MUESTRAL DE LAS
VARIANZAS
La varianza
poblacional
, donde N
es el tamaño de la población, requiere ser estimada a partir de la
varianza muestral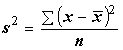 
l
Si x
se distribuye normalmente, ( x
- m )
y ( x
-
) también lo harán,
de donde 
tendrá distribución
normal ( 0, 1)
y 
tendrá
distribución z 2
o sea c
2
con 1 grado de libertad
La suma 
se
distribuirá como c
2 con
( n -1 ) grados de libertad ya que la media ()fue
calculado a partir de las observaciones de la muestra ( hay solamente n-1
observaciones independientes)
De donde 
y ns2
/ s2
se distribuye como c
2 con
( n -1 ) grados de libertad
l
Como n
= gl es el único parámetro de la distribución de c
2
, el
problema está parcialmente resuelto.
l
Sin embargo en
las aplicaciones suele ser necesario disponer de una estimación
centrada de
la varianza
(s2)
Recordemos
que una estimación (
)
de un parámetro (q
) es centrada si E()
= q
Para cada observación 
es una identidad. Por lo tanto tomando esperanzas sobre las sumas de
cuadrados:
porque los
productos cruzados se acumulan. Intercambiando los operadores E
y S
, tenemos:
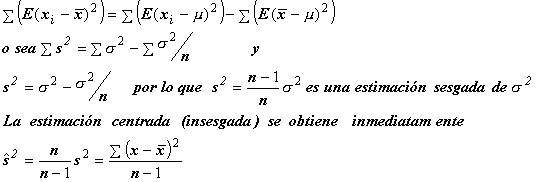
PLANES DE
MUESTREO ALEATORIO (MA)
SIMPLE
(MAS)Cada
elemento de la población tiene la misma probabilidad "a priori"
de ser incluido en la muestra
Es
el muestreo más sencillo desde el punto de vista matemático. Es costoso
y no provee información respecto a subpoblaciones
ESTRATIFICADO
(MAE)La
población se divide en subpoblaciones (estratos) identificados por
niveles en los factores. En cada estrato se realiza MAS
Se
usa cuando se desea información precisa para cada estrato o cuando
razones administrativas lo hacen conveniente
POR
CONGLOMERADO
(MC)La
población se divide en subpoblaciones (conglomerados) que se consideran
" a priori " similares en los factores. Se seleccionan
conglomerados y dentro de éstos, unidades secundarias.
Se
usa cuando es imposible o muy caro construir un marco de muestreo o cuando
los elementos están conglomerados en forma natural (p.ej. cercanía
geográfica)
SISTEMÁTICO
(MS)La
población se ordena con algún criterio (puede ser aleatorio). Se sortea
un elemento primero para ser muestreado y se continúa muestreando uno
cada tantos (paso)
( Por ejemplo 5, 15, 25,...,85)Es
fácil de realizar cuando no se dispone de identificación de los
elementos. Puede introducir variaciones cíclicas en los resultados
Si
x1,
x2,.....xn
son variables aleatorias independientes cada una con media mi
y varianza si2,
se cumple que cuando n
tiende a infinito el cociente
tiende
a distribuirse normalmente con media m=0
y varianza s2
=1, aunque
las distribuciones de las xi
sean distintas entre si
La
convergencia hacia normal de la distribución binomial
se explica por el teorema
de De Moivre que es un caso particular del teorema central del
límite
