c)
decisión z
tabulado para
0.45 = 1.645 ; b) El tamaño de
muestra requerido sería mayor o igual a 25
z tabulado
para 0.475 =
0.23 Tus
sugerencias - Página principal
- 
Spanish Banner: Intercambio de Enlaces.
inferencia: 1
muestra
ejercicios resueltos
Aplicaciones de la distribución
Normal
Aplicaciones de la distribución
de t
Verificación
de hipótesis relativas a medias
Con los mismos
datos del ejercicio anterior, se desea saber si esa muestra es compatible
con la hipótesis de que la media poblacional es 11, a nivel de
significación del 5%
a) los datos del ejercicio
=10
; s
= 3 ; n = 10 ; a
= 0.05
b)
Hipótesis a verificar :
Ho
: m
= 11
H1
: m
11 Test
a utilizar : z
z tabulado
para 0.475 = 1.96
z calculado =
10 - 11 = -
2
3 /
936
d)
conclusión : La media de la población de donde fue
extraída esa muestra no vale 11
Tamaño
de muestra para estimar medias poblacionales
¿Cuál sería
el tamaño de muestra necesario, para estimar a nivel de confianza
del 90% la media poblacional con un error menor o igual de 1 si la
desviación típica de la población es 3?
a) para un n.c. del 90%
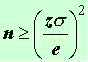
( 1.645
x 3 )2
= 24.35
1
Verificación
de hipótesis relativas a proporciones
En una muestra
de tamaño 100, se registraron 50 ocurrencias de un acontecimiento. Se
desea saber a nivel de significación del 1% si la proporción poblacional
es 0.4
a) Datos del ejercicio:
muestra n = 100 ; p = 50/100 = 0.5 ; a
= 0.01
b)
Hipótesis a verificar:
Ho
: P
= 0.4
H1
:
P0.4 c)
El test es bicaudal, z
tabulado para
0.455 =2.58
d)
z calculado
= 
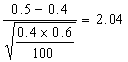
decisión:
conclusión:
la proporción
poblacional puede ser 0.4
Estimación
de proporciones poblacionales
Una muestra de
150 animales, reveló que 45 estaban enfermos. Se desea estimar la
prevalencia de esa enfermedad con una confianza del 95%
p = 45 /150 = 0.3 ; q = 1- p = 1-
0.3 = 0.7 ; n = 150
1.96
Límite de confianza inferior
Límite de confianza superior
P
0.37
Tamaño
de muestra para estimar proporciones
Determinar el
tamaño de muestra necesario para estimar una proporción poblacional a
nivel de confianza de 0.95, con un error absoluto menor que 0.05, siendo
que en una muestra piloto se obtuvo una p = 0.2
a) para
un n.c. del 95%
z tabulado
para 0.475 = 1.96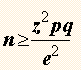 
1.96 2
x 0.2 x 0.8 = 245.86
0.052
b)
El tamaño de muestra
necesario para estimar la proporción poblacional será mayor o
igual a 246
