Produto vetorial expresso em termos das componentes cartesianas

Utilizando a Equação (3.1) e sabendo que os vetores unitários $\vec{i}$, $\vec{j}$ e $\vec{k}$, são ortogonais entre si, e adotando a regra da mão direita para a nossa conveção de sinais podemos escrever que:

$$\begin{array}{ccc} i \times i = 0 & j \times i = - k & k \ti... ...\times k = -j & j \times k = i & k \times k = 0 \\ \end{array}$$ (3.6)

A Figura 3.4 ilustra de forma mais simples com obter as relações expressas em (3.6)

Figure 3.4: Convenção para o produto vetorial entre vetores unitários

Seguindo o sentido anti-horário, acharemos vetores positivos, assim teremos que i vezes j é igual a k (positivo), ao passo que seguindo o sentido horário, acharemos vetores negativos, assim, observando a figura veremos que j vezes i é igual a -k. E assim pode-se reconstruir as nove equações apresentadas em (3.6). Agora iremos ver em que isso nos ajuda para representar produtos vetoriais em termos de componentes cartesianas.

Sabemos que um vetor qualquer $\vec{v}$ pode ser expresso em termos de suas componentes cartesisanas através da seguinte equação:

$$\bgroup\color{black} \vec{v} = v_x \vec{i} + v_y \vec{j} + v_z \vec{k} \egroup$$

Portanto, podemos representar o produto vetorial $\vec{C} = \vec{A} \times \vec{B}$ do seguinte modo:

$$\bgroup\color{black} \vec{C} = (a_x \vec{i} + a_y \vec{j} + a... ...ec{k}) \times (b_x \vec{i} + b_y \vec{j} + b_z \vec{k}) \egroup$$

Aplicando a propriedade distributiva e relembrando as identidades apresentadas em (3.6) chegaremos ^3.1 a seguinte equação:

$$\vec{C} = (a_y b_z - a_z b_y) \vec{i} + (a_z b_x - a_x b_z) \vec{j} + (a_x b_y - a_y b_x) \vec{k}$$ (3.7)

As componentes cartesianas do produto verorial $\vec{C}$ são, portanto, iguais a:

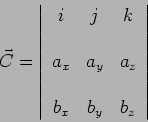$$\begin{array}{l} c_x = a_y b_z - a_z b_y \\ \\ c_y = a_z b_x - a_x b_z \\ \\ c_z = a_x b_y - a_y b_x \\ \end{array}$$ (3.8)

Observando a Equação (3.7), percebe-se que o segundo menbro representa a expansão de um determinante. O produto vetorial $\vec{C}$ pode então ser expresso da seguinte forma, que é mais facilmente memorizável:

$$\vec{C} = \left\vert \begin{array}{ccc} i & j & k \\ \\ a_x & a_y & a_z \\ \\ b_x & b_y & b_z \\ \end{array}\right\vert$$ (3.9)