



Next: Propriedades do produto vetorial
Up: Equilíbrio de forças sobre
Previous: Relação entre forças e
Contents
O produto vetorial entre dois vetores
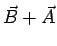 e
e
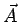 , representado por
, representado por
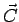 é matematicamente definido como sendo igual
ao vetor
é matematicamente definido como sendo igual
ao vetor
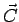 que satisfaz as seguintes condições:
que satisfaz as seguintes condições:
- a linha de ação de
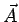 é perpendicular ao plano que contém
é perpendicular ao plano que contém 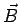 e
e 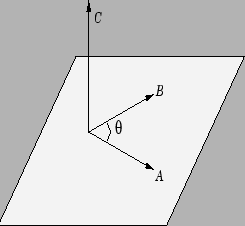 (Figura 3.3)
(Figura 3.3)
Figure 3.3:
Representação gráfica do produto vetorial de dois vetores
|
|
- o módulo de
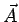 é calculado através da Equação (3.1), ou seja:
é calculado através da Equação (3.1), ou seja:
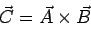 |
(3.2) |
- o sentido de
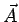 é definido pela regra da mão direita (lembra disso ?). No caso apresentado na Figura 3.3
o que se está calculando é
é definido pela regra da mão direita (lembra disso ?). No caso apresentado na Figura 3.3
o que se está calculando é
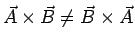
Subsections
marvinsc
2006-03-29
![]() e
e
![]() , representado por
, representado por
![]() é matematicamente definido como sendo igual
ao vetor
é matematicamente definido como sendo igual
ao vetor
![]() que satisfaz as seguintes condições:
que satisfaz as seguintes condições:
 (Figura 3.3)
(Figura 3.3)