Relação entre forças e corpos rígidos

A ação de uma força sobre um corpo rígido pode resultar em apenas três efeitos: a) ou o corpo traslada (move-se ao longo de um eixo); b) ou o corpo gira (em torno de um ponto ou em torno de um eixo); c) ou o corpo traslada e gira ao mesmo tempo.

Eis que surge uma novidade: a rotação, que não existia na relação entre forças e pontos materiais (um ponto não gira). Como dissemos acima, a rotação pode se dar em torno de um ponto, ou em torno de um eixo. Inicialmente trataremos de estudar a rotação em torno de um ponto, uma vez que tal entendimento será suficiente, por hora, para resolver nossos problemas.

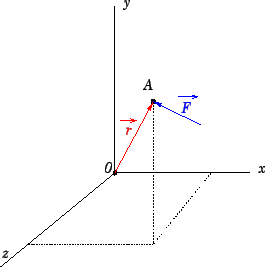A ferramenta matemática utilizada para representar o momento de uma força em torno de um ponto é o de produto vetorial. Vamos ilustrar com o esquema apresentado na Figura 3.2, onde existe uma força $\vec{F}$, um ponto $A$ e um ponto $0$ que é a origem de um sistema de eixos cartesianos.

Figure 3.2: Momento de uma força em relação a um ponto

Vamos supor que esse ponto $\vec{A}$ é a extrmidade de uma barra de ferro que tem origem no ponto $0$. Vamos supor ainda que a barra esta rotulada no ponto $0$ de modo que este ponto não possa se deslocar. Essa situação é semelhante a alguém apertando uma porca com uma chave de boca.

A força $\vec{F}$ quando aplicada na extremidade $A$ faz com que a barra de ferro tenda a girar em torno do ponto $0$, e essa quantidade que mede a tendência do giro provocado pela força $\vec{F}$ é chamada de momento da força $\vec{F}$ em torno do ponto $0$.

Portanto, para que exista momento em torno de um ponto necessáriamente tem que existir:

1. Uma força;
2. Um ponto de aplicação;
3. Um centro de giro.

Quando estávamos no segundo grau, calculávamos momento como sendo igual a força vezes distância ( $M=F \times d$). Essa equação nos induzia a pensar que momento é uma grandeza escalar, o que não é verdade. Por definição, momento é uma grandeza vetorial, resultado do produto vetorial entre dois vetores. Na realidade o que aquela nossa equação que utilizávamos durante o ensino médio nos fornecia era a intensidade do vetor momento em uma situaçaão muito particular onde o vetor posição do ponto de aplicação da força forma noventa graus com o vetor força, uma vez que a intensidade de um momento é calculada através da seguinte equação:

$$M = F \cdot d \cdot sen\, \theta$$ (3.1)

Onde $M$ é a intensidade do momento, $F$ é a intensidade da força que causa o momento, $d$ é a distância entre o ponto de aplicação da força e o centro de giro e $\theta$ é o ângulo formado entre o vetor posição do ponto de aplicação da força e o vetor força. Em (3.1) são todos escalares, de modo que essa equação somente fornece a intensidade do vetor momento. Agora que estamos estudando as relações entre forças e corpos rígidos termos que expandir um pouco mais o nosso conhecimento, e para isso precisaremos entender o que é produto vetorial de dois vetores.