Momento de uma força em relação a um ponto

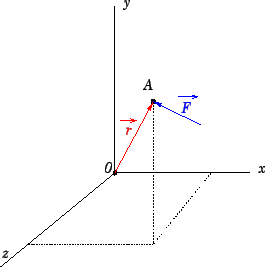
Agora que já sabemos o que é produto vetorial, o que é vetor força e o que é vetor posição vamos definir de forma mais clara o momento de uma força em relação ao um ponto: Dado um corpo rígido qualquer que possui os pontos $0$ e $A$ e uma força $\vec{F}$ qualquer aplicada sobre o ponto $A$ define-se o momento de $\vec{F}$ em relação ao ponto $0$ como sendo o seguinte produto vetorial.

$$M^{F}_{0} = \vec{r} \times \vec{F}$$ (3.10)

Onde $\vec{r}$ é o vetor posição do ponto de aplicação da força $\vec{F}$ em relação ao centro de giro $0$.

Vamos fazer umas continhas: Calcule o momento provocado pela força $\vec{F} = 150 \vec{i} + 250 \vec{j} - 100 \vec{k}$ em relação a um ponto B de coordenadas (1,2,3) sabendo que a força está aplicada no ponto A de coordenadas (3,2,1). Calcule também o momento dessa força em relação a origem. Obtenga o módulo e os cossenos diretores do vetor momento calculado em relação a B e em relação a origem.