Propriedades do produto vetorial

O produto vetorial não goza da propriedade comutativa, ou seja $\vec{A} \times \vec{B} \ne \vec{B} \times \vec{A}$. Na realidade, ao aplicarmos a regra da mão direita para definir o sentido do vetor resultante do produto, verificaremos que:

$$\vec{A} \times \vec{B} = - ( \vec{B} \times \vec{A} )$$ (3.3)

Outra propriedade que não se verifica com o produto vetorial é a propriedade associativa, ou seja:

$$(\vec{A} \times \vec{B}) \times \vec{C} \ne \vec{A} \times (\vec{B} \times \vec{C} )$$ (3.4)

A única propriedade de produtos que se verifica com o produto vetorial de dois vetores é a propriedade distributiva, ou seja:

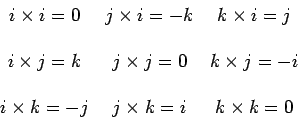$$\vec{A} \times (\vec{B} + \vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C}$$ (3.5)

E é com base na propriedade distributiva é que montamos uma equação para representar o produto vetorial em temos de suas componentes cartesianas. Vejamos como isso funciona na próxima seção.