*
* * * *
*
HERTZIAN ELECTRODYNAMICS
*
(Correction of Maxwell's equations)
The whole modern physics is based on the Newton's mechanics and Maxwellian electrodynamics. Einstein's theory of relativity serves as a connecting agency between them. The quantum physics is obtained by applying of some operators on them, while the thermodynamics and statistical physics are obtained from them using apparatus of the theory of probability and statistics.
What is a scientific theory, and what is its purpose?
Every scientific theory represents a model that alleviates understanding of a particular branch or sphere of scientific research. There is no model that can completely explain a particular area of scientific investigations, it may just give a more or less satisfactory explanation.
What is situation with the physics today?
When Newtonian mechanics emerged from the darkness of Middle Ages it served in the Age of Enlightenment as a token of human victory over nature, religious blindness and destiny. It was so influential that even today we have notion of "mechanistic theory" as a theory that explores or explains a particular phenomenon in mechanical style. But, at first Huygens and Leibnitz didn't accept Newton's law of gravitation because it implied that for example Sun acts instantaneously on Earth and other planets, or to say more scientifically, it acts instantaneously at distance. Today physicists theorize with general relativity, gravitons etc., but when they wish to make real computations they inevitably use pure Newtonian mechanics as it gives real results.
- The first postulate of relativity
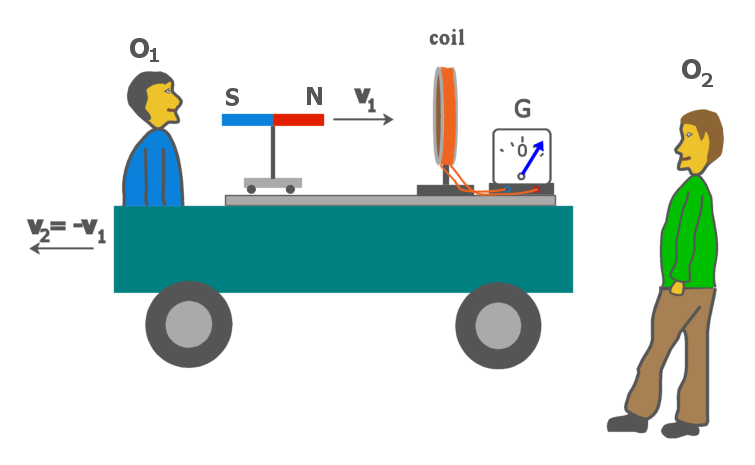
-
According to Maxwellian electrodynamics, the man in blue sweater explains the turning of the galvanometer needle by the first Maxwell's equation, while the green fellow explains the same phenomenon by the Lorentz force. According to Hertzian electrodynamics, both observers explain the phenomenon by the same law, namely Hertzian form of the first Maxwell's equation... more
By emerging of electromagnetism, the situation becomes more complicated. There happened to be many theories that explained electromagnetic phenomena. It was German physicist Wilhelm Eduard Weber who first posed on 1846 an equation of electromagnetic force between charged particles. Today, Maxwell's equations are generally accepted as the best explanation of electromagnetism. However, the situation is quite strange. Maxwell first published his equations in his article "A Dynamical Theory of the Electromagnetic Field" in 1865. There he posed a system of twenty partial differential equations and the same number of unknowns. In 1873, he published famous book "A Treatise on Electricity and Magnetism" where he posed his equations in form of five quaternion equations, but both formulations ultimately proved unpopular. It was Oliver W. Heaviside (allied with Willard Gibbs) who introduced vectors in mathematics and gave a system of four intelligible vector equations. Actually, those equations are related to vacuum and lecturers of electrodynamics usually add two equations for material media. What we call today Maxwell's equations are Heaviside's form of Maxwell's equations. Soon, it was perceived that those equations are not invariant under the Galilean transformation. It was Einstein who "solved" the problem introducing special relativity and the strange notion of "covariancy".
It is almost unknown among physicists that Jewish physicist Heinrich Hertz (his father was German Jew, converted to Christianity) posed equations of electromagnetic field, too (H.R. Hertz, Electric Waves, translated by D.E. Jones (Teubner, Leipzig, 1892; Dover, NY, 1962)). We will name them Hertz's form of ME, or simply Hertz's equations. Those equations differ from Heaviside's form of ME in just that they have total derivatives (d/dt) instead partial ones (∂/∂t) in the first end the second ME, and just for this reason they are invariant under the Galilean transformations (Phipps Thomas E. Jr, "On Hertz's Invariant Form of Maxwell's Equations", Physics Essays 6 /2 (1993) 249-256.). It means that they don't need Einstein's relativity, as far as the first postulate of relativity is concerned.
Maxwellian vs. Hertzian electrodynamics
In the following table are presented main differences between Maxwellian and Hertzian electrodynamics. Main source is the above paper of Mr. Thomas Phipps.
Maxwellian | Hertzian | Commentary |
|---|---|---|
Equations |
||
|
V
_
×E = -
∂B
___
∂t
|
V
_
×E = -
dB
___
dt
|
Due to identity:
-
dB
___
dt
= -
∂B
___
∂t
+
V
_
×(v×B),
one may see that Lorentz force is incorporated into the first Hertz's equation.
|
|
V
_
×B = μoj +
∂E
___
c2∂t
|
V
_
×B = μojr +
dE
___
c2dt
|
Due to identity:
μojr +
dE
____
c2dt
= μoj +
∂E
____
c2∂t
-
V
_
×(v×
E
__
c2
),
one may see that there is an extra component on the right side of the second Hertz's equation.
|
|
V
_
·E =
ρ
__
εo
|
V
_
·E =
ρ
__
εo
|
|
|
V
_
·B = 0
|
V
_
·B = 0
|
|
| Fq = q·(E + v×B) | Fq = q·E | Lorentz's force should be counted as the fifth Maxwell's equation. Hertzian electrodynamics retains the definitional relationship between force on a point charge and corresponding electric field |
Variables |
||
|
Nonrelativistic E = E(r, t), B = B(r, t) Relativistic E = E(r, v, t), B = B(r, v, t) |
E = E(r, v, t), B = B(r, v, t) |
In Maxwellian electrodynamics electric and magnetic fields are functions of their coordinates and time, only. However, in relativistic Maxwellian electrodynamics as well as in Hertzian electrodynamics they depend on the velocity of detector, too. |
Detectors |
||
| Infinite number of stationary detectors at every point of R3 space. Detectors are proprietary of reference frame, and every trajectory has countless number of detectors. | Only one detector for a trajectory of interest, moving with any velocity. Every particle has a role of a detector. | Electric and magnetic fields in Maxwellian electrodynamics are mathematical construction. It is the field that a particle would detect if it were stationary. In Hertzian electrodynamics they show the real field that a particle faces. |
| Every reference frame (observer) gets its own values for a field at a given point. | Every reference frame gets the same value for a field at a given point. | Even in relativistic electrodynamics every observer gets his own value for a field at a given point. |
| Every reference frame (observer) must have its own (countless) system of detectors for a trajectory. | There is a single detector for all reference frames per trajectory. | |
Conformity to the first relativity postulate |
||
| No | Yes | To be honest, even the relativistic Maxwellian electrodynamics does not conform to the first relativity principle. Physicists introduce a term covariancy, which is, actually, a euphemism for not invariant. In Hertzian electrodynamics, equations of electromagnetic field are invariant. |
Denying Newton's Third Law |
||
| Yes | No | Electromagnetism experts boast that the action-reaction law (i.e. the Newton's Third Law) is not valid in electromagnetism. Hertzian electrodynamics does not negate the action-reaction law. |
My objections to Maxwell's equations
Firstly, I will mention that Maxwell's equations fascinate (or seduce) people by some of its properties. Heaviside's form of ME fits nicely in special relativity, getting a symmetrical space-time form. Moreover, it fits nicely with Lagrangian formalism, quantum mechanics, quantum electrodynamics, quantum field theory, and as I could discern with the string theory.
However, there are many indicators of flaws in Heaviside's form of ME.
- Faraday’s law in textbooks
-
It is obvious even for undergraduate students that Faraday’s law can not be equated with the first Maxwell’s equation. However, a kind of hypnosis by authority is taking place. It seems that there is a strong psychological pyramidal pressure that creates a system of prohibitions upon subordinates, which may be an interesting theme for psychoanalysts. To my opinion, it is the same kind of pressure that was in the Middle Ages, though in milder manner. Then, the disobedient would have risk to be burnt on stake, but today, you risk not to pass exam, lose job, or to be ridiculed from the side of obedient ones. It seems that the civilization has evolved technically retaining old psychological patterns.... more
1) It may be shown that Maxwell's equations for material media (EM04HD.pdf) are spurious, due to double (mutually exclusive) definitions for (so called) "magnetic field" and "electric displacement" vectors.
2) They don't include Faraday's law of electromagnetic induction (EM05FL.pdf), as well as Lorentz force. Lorentz's force has a role of a patch for Maxwell's equations, so that it should be better named the fifth equation of electromagnetic field (In Hertzian electrodynamics, Lorentz's force is a constituent part of the first equation of the electromagnetic field).
3) The last remark relates to writers of textbooks and monographies of electromagnetism. Namely, when they deduce Maxwell's equations they don't make difference among various types of electric field, which gives space to perform some illegal derivations. As a rule, equations are derived in obscure and inconsistent manner. However, less comprehensible, more awes they get from readers.
*
The very similar situation may be found in continuum mechanics. There, we have so called material and spatial coordinates, i.e. Lagrangian and Eulerian descriptions of physical properties. "The material derivative of any such property is the time rate of change of that property for a specific collection of particles (one or more) of the continuum body. This derivative can be thought of as the rate at which Pij... changes when measured by an observer attached to, and traveling with, the particle or group of particles." (G. T. Mase and G. E. Mase, Continuum mechanics for engineers 2nd ed., 1999, CRC Press LLC)
In the material description, the material derivative is simply the partial derivative with respect to time, while the material derivative operator for properties expressed in the spatial description is the total derivative with respect to time. However, no one in continuum mechanics uses the material description and partial derivatives in practical computations. Only spacial (Eulerian) description and total derivatives are used in real situations in fluid dynamics and other area of continuum mechanics.
Hertzian electrodynamics
As it is mentioned above, we can make just a model of reality, which is and will always be unattainable and inconceivable. Every model will show sooner or later its flaws. Naturally.
Here, the equations of electromagnetic filed are derived in a simple, transparent way, starting from three simple, well-known experiments. In some places, the reader will stumble upon logical lips, which are mentioned openly, without beating about a bush or using some tricks. Those lips could be certified experimentaly, I don't have means for. Electrostatics (EM01ES.pdf) is derived in usual manner from Coulomb's law. Base equations of electromagnetic field, here named Lorentz's equations (EM02LE.pdf) are derived simply from two elementary experiments. By these equations, it is possible to give a pictorial explanation of some basic electromagnetic phenomena. Four Maxwell's equation's (EM03ME.pdf) are derived from Lorentz's equations in consistent manner. It appears that the obtained equations coincide with Hertzian form of Maxwell's equations (which I named Hertz's equations, to avoid ambiguity). From these equations it is possible to get a unique complex four-dimensional equation of electromagnetic field.
Disclaimer
I don't think that all I have written is "plain truth". I have just exposed my understanding of the matter. I am very grateful to any argued objection as well as approval.
Petrovic Branko
Email: bpshalom@yahoo.co.uk
Placed: August 2005
Updates:
November 2007 - Site completely rearanged. Added "Lorentz's Force"
December 2007 - Front page rearanged. Added table "Maxwellian vs. Hertzian electrodynamics".
January 2008 - Corrected error in documents "Maxwell's equations" and "Faraday's law" relating to conditions for surfaces of integration in integral form of Maxwell's equations.
June 2008 - Added comparison with continuum mechanics.
March 2009 - A minor revision of "Electrostatics" and "Lorentz's equations".

