Lorentz's Force
It is not necessary to ponder into subatomic realms to notice the inconsistency of Maxwell's equations. It may be shown by an elementary experiment. The experiment needs just a bar magnet, a coil and a galvanometer.
*
- Standing still galvanometer

- As it may be seen, when there is no movement of the magnet bar, there is no movement inside the galvanometer:
B = Const. --> ∂B/∂t = 0 --> E = 0.
*
- Moving bar

- Moving bar magnet generates time change of magnetic field (∂B/∂t ≠ 0).
Variable magnetic field, in turn, generates induced electric field according to the first Maxwell's equation:
V×E = -∂B/∂t,_
inside the coil that moves free electrons of the coil producing induced current through the galvanometer, whose needle is moving left and right.
*
- Moving coil

- When bar magnet stands still, there is no time variation of magnetic field and there is no induced electric field, according to Maxwell's equations:
B = Const. --> ∂B/∂t = 0 --> E = 0
However, the galvanometer needle is equally moving left and right. This phenomenon is now explained by the Lorentz's force:
F = q·v x B
that acts on free electrons of the coil.
*
This is obviously inconsistent being that the two last cases are equivalent and they should be described by same equation. According to Hertz's equations, however, both cases are described by the same equation:
and in both cases, it is the same electric field E that acts on free electrons of the coil.
*
I was very surprised when I found (thanks to Andrija Radovic's page: THEORY OF RELATIVITY - ULTIMATE DISPROOF) almost the same remarks about Maxwell's equations in the introductory statements of the famous Einstein's paper Zur elektrodinamik bewegter Körper:
ON THE ELECTRODYNAMICS OF MOVING BODIES
By A. EINSTEIN
June 30, 1905
It is known that Maxwell's electrodynamics - as usually understood at the present time - when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise - assuming equality of relative motion in the two cases discussed - to electric currents of the same path and intensity as those produced by the electric forces in the former case.
Scientists were aware of the flaws of Maxwell's equations at the beginning of the 20th century, however few of them dared to amend them. It was Hertz who proposed a variant of Maxwell's equations (H.R. Hertz, Electric Waves, translated by D.E. Jones (Teubner, Leipzig, 1892; Dover, NY, 1962).), that differed slightly from Maxwell's original form (partial derivatives were substituted by total ones), and that did not "lead to asymmetries" as mentioned by Einstein and are invariant to Galilean transformations.
*
Moving truck
Let's now append a truck to the previous experiment. Let's take into consideration that part of the case when bar magnet SN moves toward the coil, say by the velocity v1 = 3m/s. For the blue observer O1 on the illustration, the galvanometer needle turns due to induced electric field that pushes electrons in the coil. Let's now take that this observer with all his gadgets is inside a truck that moves by the opposite velocity v2 = -v1 = -3m/s. For another observer O2 outside the truck, the bar magnet is standing still, while the coil is moving toward the bar. For that observer, there is no electric field and the galvanometer needle turns due to Lorentz force. In other words, the same physical event is described by two different equations, i.e. by two different physical laws. Namely, in the first case by the low of electromagnetic induction, and in the second case by the low of Lorentz force. Thus, it is violated one of the fundamental postulate of physics:
The laws of physics are the same in all inertial frames!
Moreover, this experiment shows that Maxwellian electric field is not a physical quantity, but a mathematical construction, being that it exists for one observer and doesn't exist for another. In Hertzian electrodynamics, both observers use the same law to describe the phenomenon, and measure the same electric field.
- Moving truck
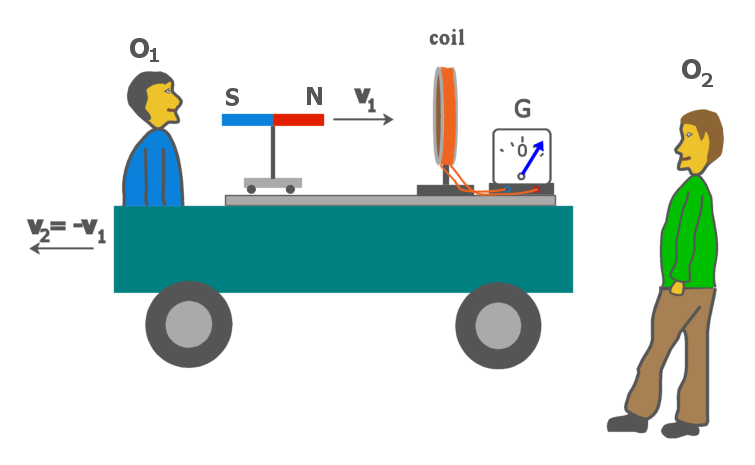
- For the observer O1 inside the truck, the bar magnet SN moves toward the coil, and accordingly, there is (Maxwellian) induced electric field around the magnet. However, for the observer O2 outside the truck, the bar magnet stands still, while the coil moves toward it, and accordingly there is nowhere induced electric field according to Maxwell's equations. In Hertzian electrodynamics, both observer O1 and observer O2 perceive the same electric field E.
Moving truck and relativity
Let's now analyze the above experiment in the light of the Special relativity. We'll start with green observer O2, being that there is no electric field in the coil for him (E2 = 0). let's now get the electric field in the coil inside the reference frame of the blue observer O1. Applying relativity transformations (Stephenson G., Kilmister C.W., Special Relativity for Physicists, Dover Publications, Inc., Mineola, N.Y., 1987., expression 6.11 on pg. 14) on E2, we get:
E1 = E2* + βv2×B/c,
where:
E2* = βE2 −(β−1)v2(v2·E2)/v22,
and
β = (1 − (v2/c)2)−1/2.
Being that:
(v2/c)2 = 10−16,
and
E2 = 0,
we get, finally:
E1 = v2×B/c.
From the just obtained results we can deduce many conclusions.
- The two fields E1 and E2 have two different values. However, nobody matters it for they are now covariant.
- If the bar magnet moved by nonuniform velocity, it would be inappropriate to use special relativity for it is valid just for uniform transformations.
- If we take a closer look at the expressions for relativistic transformation of electric and magnetic field:
E1 = E2* + βv2×B/c,
B1 = B2* − βv2×E/c,
it may be seen that they comprise just those parts missing from Maxwell's equations that are included in Hertzian equations:
V_×E = -dB___dt= -∂B___∂t+V_×(v×B),V_×B = μojr +dE____c2dt= μoj +∂E____c2∂t-V_×(v×E__c2). - It seems to me that this coincidence is the main reason why the relativity gives satisfactory results, even in quantum mechanics where the particles movings are far from uniform.
*
A weird experiment that has changed the face of Physics
One may asks now: "Why all this fuss? Why did not Maxwell take total derivatives instead of partial ones?"
As I could discern, the answer is bizarre.
At the very beginning of his investigations, Michael Faraday stumbled upon a totally weird experiment, known as "homopolar generator". I will only mention that this experiment has been making headache to physicists since (if someone is interested on the subject, just google little bit with this expression, and you will reveal a heap of relevant materials). I am suggested (Andrija Radovic) that it was this experiment that led Maxwell to take partial derivatives instead of total ones.
It is unbelievable that such an experiment could have such tremendous impact on the science. The fact is that Hertzian form of Maxwell's equations does not need Einstein's relativity. On the other hand, Joseph A. Rybczyk (yet another heretic) proved that Lorentz transformations and other relativistic equations could be derived just from the independency of light speed from the velocity of its source.
*
*
Some links to homopolar generators:
Wikipedia
THE ROTATION OF MAGNETIC FIELD
Andrija Radovic
THE WEIRD BUBBLE
*
*

