



Next: Parâmetros iniciais
Up: Centróides e Baricentros
Previous: Baricentros de áreas compostas
Contents
Outra forma para determinar a posição do centróide de figuras planas consiste na integração direta das Equações (6.7).
Neste caso é necessário se conhecer as equações das linhas que definem o contorno da superfície. Vamos a um exemplo de modo a
ilustrar o procedimento: Digamos, por exemplo, que desejamos calcular o baricentro da superfície apresentada na Figura 6.6.
Figure 6.6:
aula 6 - exemplo 3
|
|
Para facilitar nossos cálculos vamos admitir que
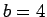 ,
,
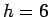 e
e
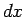 . Existem diferentes modos de se obter o valor das integrais (6.7),
e o que vamos apresentar agora é apenas um deles:
. Existem diferentes modos de se obter o valor das integrais (6.7),
e o que vamos apresentar agora é apenas um deles:
- Escolhe-se uma faixa de largura
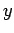 , paralela ao eixo
, paralela ao eixo 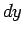 ou uma faixa de largura
ou uma faixa de largura 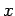 , paralela ao eixo
, paralela ao eixo 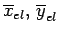 .
.
- Calcula-se a posição do centróide dessa faixa (
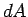 ) em relação ao sistema de eixos de referência.
) em relação ao sistema de eixos de referência.
- Escreve-se a expressão que define a área
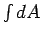 , da faixa escolhida
, da faixa escolhida
- Calcula-se a área, através da integral
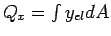
- Calculam-se os momentos de primeira ordem
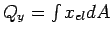 e
e
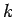
- Calcula-se a posição do centróide
Vamos então aplicar a sequência de cálculo apresentada acima:
Subsections




Next: Parâmetros iniciais
Up: Centróides e Baricentros
Previous: Baricentros de áreas compostas
Contents
marvinsc
2006-03-29
![]() ,
,
![]() e
e
![]() . Existem diferentes modos de se obter o valor das integrais (6.7),
e o que vamos apresentar agora é apenas um deles:
. Existem diferentes modos de se obter o valor das integrais (6.7),
e o que vamos apresentar agora é apenas um deles: