Baricentros de áreas compostas

Vamos analisar agora um procedimento muito utilizado na detreminação de baricentros e centróides de superfícies planas. Tal procedimento consiste em dividir uma superfície em outras menores cujas coordenadas dos baricentros sejam facilmente determinadas, ou até mesmo, previamente conhecidas. A Figura 6.3 ilustra bem o processo.

Figure 6.3: Centróide a partir da decomposição em figuras plana

Dividindo a figura maior em outras menores, cujas áreas e os centróides são facilmente obtidos, podemos lançar mão da forma discreta das Equações (6.7) e escrever que:

$$\begin{array}{l} \\ \overline{x} = \frac{\sum \overline{x}_... ... \frac{\sum \overline{y}_i A_i}{\sum A_i} \\ \\ \end{array}$$ (6.11)

Onde no caso específico do exemplo apresentado $i$ varia de $1$ a $3$, uma vez que a figura maior foi dividida em um retângulo e dois triângulos retângulos, figuras estas cuja a determinação dos baricentros e das áreas é simples e direta.

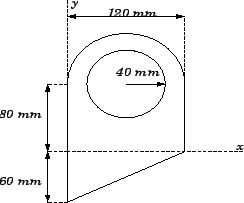
Existem tabelas de onde se pode retirar as coodenadas da maioria das figuras geométricas mais simples, nos permitindo usar do artifício da decomposição de uma superfície plana em figuras mais simples onde os valores de área e coodenadas dos centróides já são previamente conhecidos. Agora vamos exercitar um pouco esse procedimento, caculando a posição dos baricentros das superfícies apresentadas nas Figuras 6.4 e 6.5.

Figure 6.4: aula 6 - exemplo 1

Figure 6.5: aula 6 - exemplo 2