Inicialmente, consideraremos uma placa horizontal, conforme a mostrada na Figura 6.1. Podemos dividir essa placa em
![]() elementos infinitesimais, de modo que cada um desses elementos tenha um peso
elementos infinitesimais, de modo que cada um desses elementos tenha um peso
![]() , e coordenadas
, e coordenadas
![]() e
e
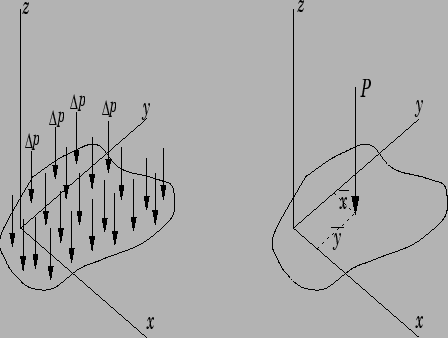 .
.
Apesar da curvatura da terra, vamos considerar que para todos os efeitos práticos essas
![]() forças
forças
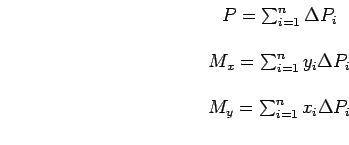 são paralelas
entre si. Sendo assim, podemos reduzir o sistema com
são paralelas
entre si. Sendo assim, podemos reduzir o sistema com
![]() forças para um que possua apenas uma única força e dois momentos,
através das seguintes equações:
forças para um que possua apenas uma única força e dois momentos,
através das seguintes equações:
Na Equação 6.1 os momentos
![]() e
e
![]() são chamados de momentos de primeira ordem da superfície em relação aos eixos
são chamados de momentos de primeira ordem da superfície em relação aos eixos
![]() e
e
![]() . Os momentos de primeira ordem medem a tendência de giro de uma superfície em relação a um eixo qualquer, contido no
mesmo plano dessa superfície.
. Os momentos de primeira ordem medem a tendência de giro de uma superfície em relação a um eixo qualquer, contido no
mesmo plano dessa superfície.
Agora, nos resta descobrir, a intensidade e o ponto de aplicação de uma única força
![]() que seja equivalente ao sistema que contém
todas as
que seja equivalente ao sistema que contém
todas as
![]() forças
forças
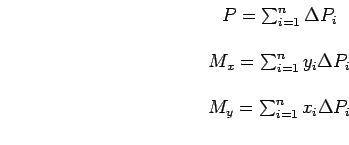 . Para que seja equivalente esse força
. Para que seja equivalente esse força
![]() deve provocar os mesmos efeitos sobre a superfície que os
provocados pelas
deve provocar os mesmos efeitos sobre a superfície que os
provocados pelas
![]() forças
forças
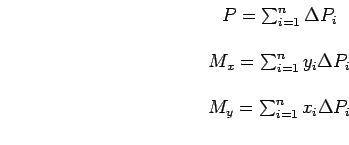 . Supondo que as coordenadas que definem o ponto de aplicação da força
. Supondo que as coordenadas que definem o ponto de aplicação da força
![]() sejam dadas por
sejam dadas por
![]() e
e
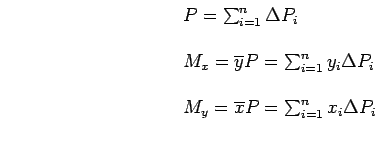 , podemos escrever que:
, podemos escrever que:
Fazendo
![]() tender ao infinito, podemos reescrever as Equações (6.2) do seguinte modo:
tender ao infinito, podemos reescrever as Equações (6.2) do seguinte modo:
A partir das Equações (6.3) podemos obter as coordenadas (
![]() ) do Baricentro G
da superfície plana. Como podemos perceber as coodenadas do baricentro dependem apenas da geometria do problema, independendo
do tipo de material que constitui a placa.
) do Baricentro G
da superfície plana. Como podemos perceber as coodenadas do baricentro dependem apenas da geometria do problema, independendo
do tipo de material que constitui a placa.
Como estamos tratando com superfícies planas, podemos expresar o peso em função da área, através da seguinte equação:
Onde
![]() é a espessura da placa, considerada constante,
é a espessura da placa, considerada constante,
![]() é o peso específico do material que constitui a placa e
é o peso específico do material que constitui a placa e
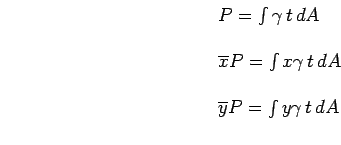 é uma área infinitesimal de um elemento tomado sobre a placa. Considerando agora a Equação (6.4) podemos reescrever as
Equações (6.3) do seguinte modo:
é uma área infinitesimal de um elemento tomado sobre a placa. Considerando agora a Equação (6.4) podemos reescrever as
Equações (6.3) do seguinte modo:
As Equações (6.5) nos permitem então calcular as coordenadas (
![]() ) do Centróide da superfície
plana considerada. Considerando o material homogêneo e a espessura da placa constante, podemos simplificar as Equações (6.5) da
seguinte forma:
) do Centróide da superfície
plana considerada. Considerando o material homogêneo e a espessura da placa constante, podemos simplificar as Equações (6.5) da
seguinte forma:
Portanto, podemos escrever que as coordenadas do centróide de uma superfície plana homogênea e de espessura constante podem ser dadas pelas
seguintes equações:
Analogamente, podemos deduzir as equações que definem a posição do centróide de um fio qualquer contido em um plano, do seguinte modo:
Onde
![]() é o comprimento de um elemento infinitesimal tomado sobre o fio. Note que na maioria dos casos, o centróide dos fios não estão
contidos nos próprios fios, e que no caso das superfícies planas, o centróide pode também não estar contido sobre o corpo definido pela
superfície, principalmente nas superfícies vazadas. Perceberemos isso mais atententamente quando entendermos melhor o conceito de centróide.
é o comprimento de um elemento infinitesimal tomado sobre o fio. Note que na maioria dos casos, o centróide dos fios não estão
contidos nos próprios fios, e que no caso das superfícies planas, o centróide pode também não estar contido sobre o corpo definido pela
superfície, principalmente nas superfícies vazadas. Perceberemos isso mais atententamente quando entendermos melhor o conceito de centróide.