Mais adiante veremos como utilizar o produto escalar no cálculo do momento de uma força em torno de um eixo. Vamos aproveitar agora, algumas aplicações imediatas para o produto escalar entre dois vetores. A primeira, e mais visível utilização consiste na determinação do ângulo formado entre dois vetores dados pelas sua componentes cartesianas, senão vejamos: Comparando as Equações (4.1) (4.6), podemos escrever que:
| (4.7) |
O que nos leva a concluir que o ângulo
![]() , formado entre
, formado entre
![]() e
e
![]() pode ser dado pela seguinte expressão:
pode ser dado pela seguinte expressão:
| (4.8) |
Uma segunda aplicação imediata de produto escalar consiste em determinar o valor da projeção de um vetor sobre um eixo qualquer.
Para entender melhor essa aplicação vamos admitir a existência de um vetor espacial
![]() qualquer, e um seguimento de reta
qualquer, e um seguimento de reta
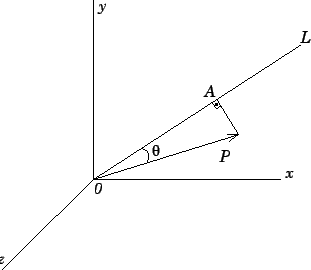 ,
também espacial e qualquer, conforme mostra a Figura 4.1.
,
também espacial e qualquer, conforme mostra a Figura 4.1.
Se quisermos obter a projeção do vetor
![]() sobre o eixo
sobre o eixo
 basta calcular
basta calcular
![]() . Assim, chamando de
. Assim, chamando de
![]() , o tamanho da projeção do vetor
, o tamanho da projeção do vetor
![]() sobre o eixo
sobre o eixo
 , temos que:
, temos que:
| (4.9) |
Consideremos agora, um vetor
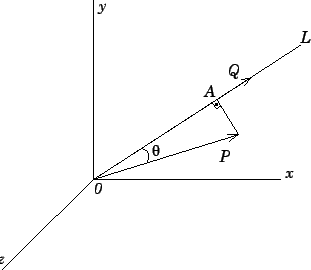 , orientado segundo o eixo
, orientado segundo o eixo
 , e com mesmo sentido que
, e com mesmo sentido que
 , conforme mostra a Figura
4.2.
, conforme mostra a Figura
4.2.
Podemos então escrever o produto escalar entre
![]() e
e
 do seguinte modo:
do seguinte modo:
| (4.10) |
E como
![]() , temos que:
, temos que:
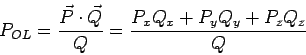 |
(4.11) |
De onde deduzimos que:
| (4.12) |
Agora, se ao invés de escolher
 sobre o eixo
sobre o eixo
 , tivéssemos escolhido, sobre o eixo
, tivéssemos escolhido, sobre o eixo
 , um vetor unitário
, um vetor unitário
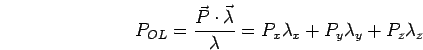 , chegaríamos
a seguinte expressão:
, chegaríamos
a seguinte expressão:
E como
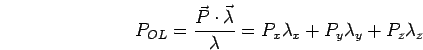 é um vetor unitário no mesmo sentido e direção de
é um vetor unitário no mesmo sentido e direção de
 , a Equação (4.13) nos dá o tamanho da
projeção do vetor
, a Equação (4.13) nos dá o tamanho da
projeção do vetor
![]() sobre o eixo
sobre o eixo
 .
.