Produto escalar em termos das componentes cartesianas

Antes de expressarmos o produto escalar em termos das componentes cartesianas vamos nos ater ao que acontece quando estamos efetuando produtos escalares entre os vetores unitários $\vec{i}$, $\vec{j}$ e $\vec{k}$. A partir da própria definição de produto escalar, e lembrando que os vetores $\vec{i}$, $\vec{j}$ e $\vec{k}$ são ortogonais entre si, podemos escrever que:

$$\begin{array}{ccc} \vec{i} \cdot \vec{i} = 1 & \vec{j} \cdot... ...} \cdot \vec{k} = 0 & \vec{k} \cdot \vec{i} = 0 \\ \end{array}$$ (4.4)

Bom, feita essa pequena observação, vamos agora ao produto escalar em termos das componentes cartesianas dos vetores, desse modo, podemos representar 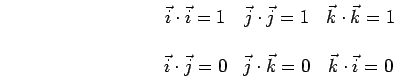$\vec{A} \cdot \vec{B}$ da seguinte forma:

$$\vec{A} \cdot \vec{B} = (A_x \vec{i} + A_y \vec{j} + A_z \vec{k}) \cdot (B_x \vec{i} + B_y \vec{j} + B_z \vec{k})$$ (4.5)

Aplicando a propriedade distributiva e lembrando das Equações (4.4), chegaremos a seguinte equação:

$$\vec{A} \cdot \vec{B} = A_x B_x + A_y B_y + A_z B_z$$ (4.6)