Produto escalar de dois vetores

O produto escalar entre dois vetores $\vec{A}$ e $\vec{B}$ é definido como sendo o produto entre os módulos de $\vec{A}$ e $\vec{B}$ e o coseno do ângulo formado entre os vetores, assim:

$$\vec{A} \cdot \vec{B} = AB \, cos \, \theta$$ (4.1)

Perceba que a notação de produto escalar entre vetores ( $\cdot$ ) é diferente da notação de produto vetorial ( $\times$ ). Quando estamos trabalhando apenas com escalares tanto faz uma quanto a outra, porém, com vetores, as notações conduzem a resultados bastante diferentes. O produto escalar, como o próprio nome já indica tem como resultado um escalar, daí já pode-se deduzir que atende a propriedade comutativa, ou seja:

$$\vec{A} \cdot \vec{B} =\vec{B} \cdot \vec{A}$$ (4.2)

Também pode-se provar que o produto escalar entre dois vetores atende a propriedade distributiva, ou seja:

$$\vec{A} \cdot ( \vec{B} + \vec{C} ) = \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C}$$ (4.3)

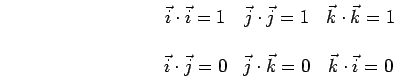A propriedade associativa não pode ser aplicada a produtos escalares de vetores $(\vec{A} \cdot \vec{B}) \cdot \vec{C}$, uma vez que $\vec{A} \cdot \vec{B}$ já é um escalar, fazendo com que a operação inicial se transforme no produto de um escalar por um vetor.