Introdução ao Método da Flexibilidade - Abordagem Geral

Inicialmente veremos os fundamentos teóricos do método da flexibilidade, que pode ser utilizado na solução de qualquer método estaticamente indeterminado, ou seja, toda vez que existirem mais forças incógnitas do que equações de equilíbrio disponíveis para a solução do problema.

Para enteder o mecanismo de funcionamento do método, vamos inicialmente analisar a viga apresentada na Figura 17-(a).

Com a finalidade de poupar tempo e também evitando reinventar a roda, adotaremos a nomeclatura semelhante a utilizada por [Gere e Weaver 1981] na denominação de ações, reações, deslocamentos e matrizes em geral. Assim que os termos forem surgindo na solução do problemas, iremos nominando os termos que se fizerem necessários.

Observando a estrutura apresentada na Figura 17-(a), vemos que trata-se de uma estrutura plana com quatro reações de apoio possíveis. A partir de agora, convencionaremos representar as reações de apoio, através de um traço cortando a força ou binário que a constitui, isso diferenciará as ações das reações.

Como a viga da Figura 17-(a) é uma estrutura plana, significa que existem três equações de equilíbrio possíveis para resolver o problema, ao passo que a mesma estrutura apresenta quatro reações de apoio incógnitas, o que torna a estrutura estaticamente indeterminada do primeiro grau, e dizemos então que a estrutura possui um redundante estático, que pode ser obtido a partir da quebra de qualquer um dos vínculos (restrição ao deslocamento nos apoios) da estrutura.

Na solução via método da flexibilidade, quebra-se um dos vínculos nos apoios, e para manter a compatibilidade da estrutura acrescenta-se o redundante estático equivalente ao vínculo rompido, que é a própria reação de apoio do vínculo que foi rompido. Qualquer um dos vínculos pode ser rompido, mas no caso dos quatro vínculos apresentados na Figura 17-(a), optou-se por romper o vínculo que impedia o deslocamento vertical no ponto B da viga, fazendo com que a estrutura assuma a forma apresentada na Figura 17-(b).

Figura: Exemplo de aplicação do Método da Flexibilidade

Como a viga da Figura 17-(a) era estaticamente indeterminada do primeiro grau, ao se romper um vínculo obteve-se a estrutura estaticamente determinada (isostática) apresentada na Figura 17-(b). Porém, ao se romper um vínculo é mandatório que se aplique o redundante estático na estrutura na mesma direção e sentido da reação do apoio rompido, aplica-se o redndante $R_B$ como o indicado na Figura 17-(c).

Desse modo, podemos representar os efeitos globais da viga da Figura 17-(a) como sendo a soma dos efeitos isolados das vigas das Figuras 17-(b) e 17-(c).

Agora, para determinar o valor da redundante $R_B$, calcularemos o deslocamento em B, para os casos das vigas das Figuras 17-(b) e 17-(c). O cálculo desses deslocamentos é geralmente realizado através do método da carga virtual unitária, tal qual foi realizado na seção 1.7.1. Aplicando a mesma técnica, obtemos o valor de $$\Delta_B = \frac{wL^4}{8EI}$$ (positivo no sentido indicado na Figura 17-(d)). 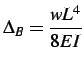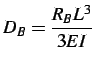Da mesma forma, para a viga da Figura 17-(b) obtemos o valor de $$D_B = \frac{R_B L^3}{3EI}$$, positivo no sentido indicado pela Figura 17-(e).

Agora, convencionaremos que o sentido da redundante será sempre positivo, e também que os deslocamentos no sentido da redundante serão sempre positivos. Após adotar essa convenção escrevemos a equação de compatibilidade do nó B da estrutura da viga original, apresentada na Figura 17-(a). Sabemos portanto que o deslocamento vertical do nó B da Figura 17-(a) é nulo, o que nos permite escrever a Equação (2.1):

$$D_B - \Delta_B = 0 \Rightarrow D_B = \frac{R_B L^3}{3EI} - \frac{wL^4}{8EI} = 0$$ (36)

Isolando o valor de $R_B$ na Equação (2.1), teremos o valor do redundante estático dado por:

$$R_B = \frac{3}{8} wL$$ (37)

Como a estrutura é estaticamente indeterminda do primeiro grau, ao se obter o valor de um redundante estático ($R_B$), pode-se agora obter as demais reações de apoio através das três equações de equilíbrio disponíveis para a viga plana.

A Equação (2.1) que permitiu a solução do problema é chamada de equação de compatibilidade, uma vez que determina os valores de deslocamentos em nós da estrutura. É esta equação que exprime a condição de compatibilidade de que o deslocamento vertical do nó B deve ser nulo, e a partir dessa equação é que obtemos o valor de um redundate estático que nos dá a solução do problema, uma vez que conhecido o valor de um redundante, as demais reações incógnitas podem ser obtidas através das três equações de equilíbrio disponíveis para estruturas planas.

Podemos ainda desenvolver uma solução mais sistemática que nos permita chegar no mesmo valor de $R_B$. Esta sistematização nos permitirá expressar as equações de equilíbrio e compatibilidade em termos gerais e matriciais, caminhando assim no sentido da generelização matricial que utilizaremos na análise das estruturas.

Um primeiro passo a ser dado no sentido dessa sistematização, é descobrir qual é o deslocamento $\delta$ no mesmo sentido e direção da redundante estática, quando aplicamos no lugar da redundante uma carga unitária, como indicado na Figura 17-(f). Desse modo, podemos expressar o valor do deslocamento $D_B$, causado por $R_B$ como sendo o produto da força redundante $R_B$ pelo deslocamento causado por uma força unitária, assim teríamos que $D_B=\delta R_B$. Com essa nova abordagem, a Equação de compatibilidade (2.1) pode ser reescrita na forma da Equação (2.3):

$$- \Delta_B + \delta R_B = 0$$ (38)

Na Equação (2.3) $\Delta_B$ é o deslocamento no ponto B, causado pela Ação $w$ na estrutura liberada. É tomado negativo porque é contrário ao sentido da redundante no ponto B. Enquanto $\delta$, representa um coeficiente de flexibilidade, uma vez que é o deslocamento provocado por uma ação unitária no ponto B, e numa forma mais geral denotamos pelo símbolo F. O termo nulo a direita da igualdade é a condição de compatibilidade que determina qual deve ser o deslocamento do nó B, que em numa forma mais geral denotamos por $\delta_B$, assim, podemos reescrever mais uma vez a Equação (2.3) na forma generalizada apresentada pela Equação (2.4):

$$\delta_B = \Delta_{B} + F \; R_B$$ (39)