Coeficientes de Flexibilidade e Rigidez

Os princípios descritos para a mola são válidos para toda e qualquer estrutura que se desloca em regime linear elástico quando solicitada por uma única ação, o que nos permite distender os conceitos de flexibilidade e rigidez de mola para os conceitos de flexibilidade e rigidez de elementos estruturais, e por consegüinte, de estruturas. Vejamos o caso da estrutura apresentada na Figura 13.

Figura: Barra sujeita a tração

No caso da Figura 13 temos uma barra engastada em uma extremidade e solicitada em outra extremidade por uma ação $A$, posicionada na mesma direção do eixo longitudinal da viga. Sabemos, da Resistência dos Materiais, que para o caso da barra da Figura 13, o deslocamento axial $\delta$ e dado por:

$$\delta = \frac{AL}{E \alpha}$$ (16)

Onde:

• $\delta$ é o deslocamento provocado pela ação $A$;
• $L$ é o comprimento da barra;
• $E$ é o módulo de elasticiade longitudinal do material que constitui a barra, e
• $\alpha$ é a área da seção transversal da barra.

Se fizermos $A=1$ na Equação (1.16) teremos o valor do deslocamento $\delta$, provocado por uma ação unitária, ou em outros termos, a flexibilidade da barra quando submetida a ações normais aplicadas no eixo da mesma. Assim, a flexibilidade $F$ de uma barra prismática submetida a uma ação normal aplicada no seu eixo longitudinal é descrita através da Equação (1.17).

$$F = \frac{L}{E \alpha}$$ (17)

Como já sabemos que a rigidez é o inverso da flexibilidade podemos também obter o valor da rigides $S$ para a barra da Figura 13, conforme expresso na Equação (1.18).

$$S = F^{-1} = \left(\frac{L}{E \alpha} \right)^{-1} = \frac{E \alpha}{L}$$ (18)

Uma vez que obtivemos $F$ e $S$ podemos agora relacionar as ações e os deslocamentos para o caso da Figura 13 em termos de sua rigidez ou de sua flexibilidade ao deslocamento longitudinal provocado por uma ação normal, na forma das Equações (1.19)

$$\begin{array}{l} \delta = F A \\ A = S \delta \\ \end{array}$$ (19)

As Equações (1.19) são as iguais as Equações (1.13) e (1.14), só que neste caso, os valores de $F$ e $A$ foram obtidos para uma situação estrutural específica. Veremos mais adiante que $F$ e $A$ são respectivamente chamados de coeficiente de flexibilidade e coeficiente de rigidez, e que sua determinação depende de técnicas específicas para cada tipo de situação estrutural. Veremos ainda mais adiante, várias formas de se obter esses valores utilizando o princípio dos trabalhos virtuais e a técnica da carga virtual unitária

Vejamos agora o caso da viga engastada apresentada no esquema estrutural da Figura 14

Figura: Viga em balanço com ação na extremidade

Agora, ao invés de tracionar a barra, a ação na extremidade provoca a flexão da barra. Neste caso, o deslocamento vertical $\delta$ indicado na Figura 14 pode ser obtido via técnica da carga virtual unitária, utilizando o princípio dos trabalhos virtuais, sendo expresso por:

$$\delta = \frac{1}{EI} \int M \overline{M} ds$$ (20)

Onde:

• $E$ é o módulo de elasticidade longitudinal do material que constitui a barra

• $I$ é o momento de inércia da seção transversal em relação a sua linha neutra

• $M$ é a expressão que define o valor dos momentos fletores reais

• $\overline{M}$ é a expressão que define o valor dos momentos fletores virtuais

Admitindo um sistema de coordenadas com origem na extremidade onde a ação $A$ está aplicada, teremos as seguintes expressões de momento:

$$\begin{array}{lr} M(x) = - A \cdot x & (0 \le x \le L) \\ \overline{M}(x) = - 1 \cdot x & (0 \le x \le L) \\ \end{array}$$

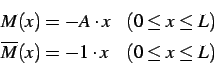
Multiplicando $M(x)$ por $\overline{M}(x)$, teremos que:

$$\delta = \frac{1}{EI} \int_0^L A \; x^2 dx = \frac{AL^3}{3EI}$$

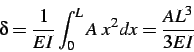
Desse modo, obtivemos o valor do deslocamento vertical $\delta$ na extremidade da viga provocado pela a ação A.

$$\delta = \frac{AL^3}{3EI}$$ (21)

Agora, para o caso da viga na Figura 14, se quisermos saber qual é o deslocamento $\delta$ provocado por uma ação unitária na extremidade onde atua a ação $A$, basta fazer $A=1$ na equação 1.21, e ficaremos com:

$$\delta = \frac{1\;L^3}{3EI} \Longrightarrow \delta = \frac{L^3}{3EI}$$

E como o valor do deslocamento $\delta$ provocado por uma ação unitária é definido como sendo a flexibilidade $F$, temos que para o caso do deslocaemento $\delta$ indicado na Figura 14, a flexibilidade ($F$) é dada por:

$$F = \frac{L^3}{3EI}$$ (22)

Sabendo o valor da flexibilidade expressa na Equação (1.22), podemos relacionar ação e deslocamento na forma expressa na Equação (1.23):

$$\delta = F \; A$$ (23)

Agora, se quisermos saber qual é a força necessária para provocar um deslocamento unitário basta fazer $\delta = 1$ na Equação 1.21, e ficaremos com:

$$1 = \frac{AL^3}{3EI} \Longrightarrow A = \frac{3EI}{L^3}$$

E como o valor da força $A$ que provoca um deslocamento unitário é definido como sendo a rigidez ($S$), temos que para o caso do deslocaemento $\delta$ indicado na Figura 14, a rigidez ($S$) é dada por:

$$S = \frac{3EI}{L^3}$$ (24)

Sabendo o valor da rigidez expressa na Equação (1.24), podemos relacionar ação e deslocamento na forma expressa na Equação (1.25):

$$A = S \; \delta$$ (25)

As Equações (1.25) e (1.23) são respectivamente iguais as Equações (1.13) e (1.14), com a diferença que desta vez, para o caso específico da barra apresentada na Figura 14, obtivemos os coeficientes de flexibilidade e de rigidez utilizando o princípio dos trabalhos virtuais.