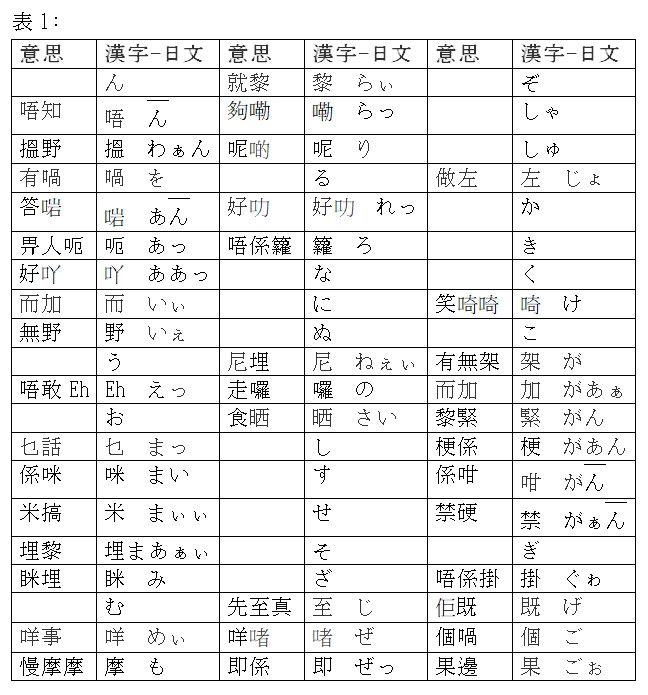
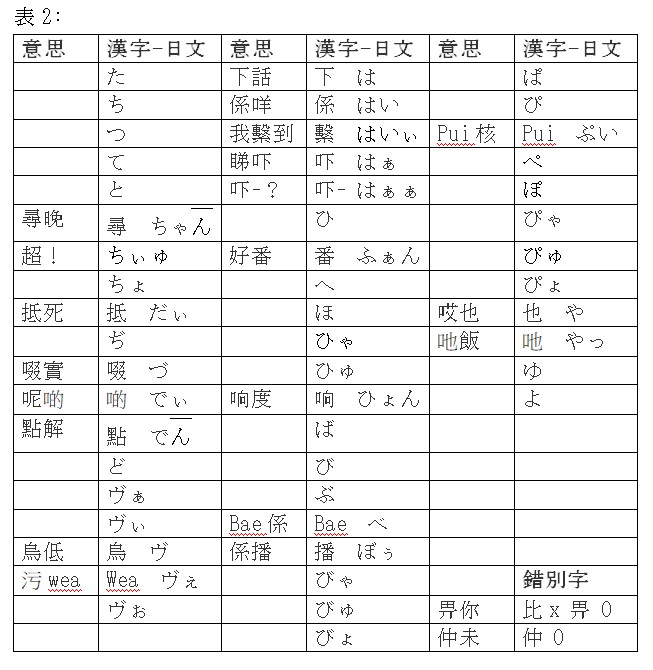
日文作句7
Topic: 13日文Japanese
お金のためにかがみ、何でも言わないにここに留まるのは、気骨なし!
ー
為じょ五斗米折腰,留はいぃ度まっ都ん敢講,無骨氣!
これならあなたと妻子と子子孫孫と一緒に、裏面の十四億ものの同じように、毎日嘘をつくったり、人々は偽物を作ったり、お金ばかりを言ったりして、ゴミに変わって待っていますよ!
ー
がん你就等你同你でぃ老婆仔女子子孫孫一齊,慢慢變到同入面個十四億いぇ一樣,變做日日講大話,個個做假いぇ,淨はい識講錢げ廢物啦!
日文作句6
Topic: 13日文Japanese
心のなかに鬼がいると、鬼がいない物はあるか?
心中有鬼,有乜いぇ無鬼吖?仆街ぞん國鬼!人渣こん產狗!賤種だい陸はい!
心のなかに香港がいると、どこまでも香港です!
人間は気骨があると、どこまでも人間としての資格があります!
心中有香港,去到邊度都はい香港!
做人有骨氣,去到邊度都有資格做人!
日文作句5
Topic: 13日文Japanese
何百年も前の人は一文なしとか、文字が知らないとかまま東南アジアやサンフランシスコまで海洋を渡り行きましたね!
幾百年前でぃ人,身無分文,盲字都唔識,都はいかん漂洋過海去到南洋舊金山啦!
あなたはたくさんの知識を身につけるし、金もあるし、恐れる必要じゃないじゃないか?
ー ー ー ー
你讀かん多書,又んはい仙都ん仙はあ,你んはい驚は話?!
子豚を売られるじゃなくて、逆に生きられる道を送りあげた。なぜここに泊まって死に待ってのを選ぶか?
ー
んはい賣你豬仔,而はい畀條生路你行呀,你揀留はぃ度等死?
日文作句4
Topic: 13日文Japanese
ここに金持ちまたは裏に大金持ちより、どこへ行っても、たとえ乞食になるまたは飢え死にしてしまうはもっと喜ぶ!
去邊度都好,就算乞食,就算餓死,都開心過はい度做有錢佬,はい入便做大富豪!
日文作句3
Topic: 13日文Japanese
私はわけが話さない人とわけを話さない。息が無駄だ。
ー ー
我ん會同ん講道理げ人講道理.さい氣!
わけが話さない人にわけを話されて待っていますか?愚かしくないでください!全くの妄想!
ー ー
等ん講道理げ人同你講道理?ん好傻啦!妄想!
日文作句2
Topic: 13日文Japanese
逃げる機会あるも去らなかったら、四苦八苦に逃げられたの父母と父方の祖父母と母方の祖父母に、どう向き合うの?とても親不孝なぁ!
ー ー
有得走ん走,でん對得住千辛萬苦至走得甩げ老豆老母阿爺阿嫲阿公阿婆呀?不孝呀!
逃げる機会あるも去らなかったら、後悔しないでください。逃げる機会もうなくなったら、どうしたら逃げられかが問い合わせないでください!
ー ー ー ー ー
有得走ん走,かん你就ん好後悔,ん好無得走先らい問人でん樣走!
日文作句1
Topic: 13日文Japanese
たとえ本当の事を言っても、誰も信じてくれないことを責めない。たくさんの嘘から誰も信じてくれないのせいで自らを責めよう。
ー ー ー
ん好怪人地でん解就算講真話都ん信你,要怪就怪你自己講太多大話搞到無人信!
オオカミが来た”この物語が、宇宙中のすべてのバージョンを、全部消してしましょう!愚か!
鏟さい全宇宙所有版本げ狼來了あ笨!
単語の作り方
Topic: 13日文Japanese
二、三千年前、中国語はだいたい一個字一個字使います。単語はあまりありません。しかし同音字がある。時間に経ってもっと字があるになった。同音字ももっとあるになった。話し時は意味が間違う易い。だから違う発音の単語が作ります。違う意味の単語を違う発音になったら、意味の間違うが易くないになっていた。
香港語は同音字があるが、同音単語は少ない。これは正しいの単語の作り方です。今は、日本語、韓国語、ベトナム語もたくさんの同音単語がある。なぜなら、直接的に漢字を使われます。従って、直接的に漢字を使われるのは絶対的な間違えた。
ちなみに、中国語もたくさんの同音単語がある。意味は分かりますか?ふんふんふん!!!
2020年12月06日
百越話假借字
Topic: 13日文Japanese
百越話,即係廣東話同粵語呢兩個名想隱藏係背後,唔想比人篤爆既真相!
假借漢字寫既越南文,同假借法文寫既越南文,都係越南文.
假借漢字寫既韓文,同用韓字寫既韓文,都係韓文.
假借漢字寫既日文,同用平假名寫既日文,都係日文.
所以, 假借漢字寫既百越話, 假借英文寫既百越話,同假借日文寫既百越話,都係百越話!唔係中文!絕對唔係!
以後都用日文寫百越話,吹咩!
順便講句,原來越南人叫越南話做(言越,Tiếng Việt),唔係(言越南),哈哈!
未寫既,第時再寫.
2020年9月15日
質數第5回
Topic: 9亂證 Crazy Proof
請先看<提示>.
事情:質數無限.
問題1:如何尋找超大質數.
問題2:如何使用質數數式.
解題:
-----------
綜合之前的結果,
P=(1+2n)3+(Y-3n)2
當n=0,
P=3+2Y
同時
P=(1+2n)(3+2j)=3+2Y
Y=(P-3)/2 ----------(17)
另外,
j=(Y-3n)/(1+2n),
j(1+2n)=Y-3n
所以,
P=3+2Y 與 Y-3n 同時是 1+2n 的倍數.
只要 Y-3n=j(1+2n), j與n有正整數解, P=(1+2n)(3+2j) 就是合成數,不是質數.
如果不繪圖,要證明 j=(Y-3n)/(1+2n) 沒有整數解,當然非常費時.
不過,現在超級電腦已經找到2千幾萬個位的質數,亦即是這個質數以下的單數,那些是質數,那些是合成數,已經有數據記錄.
既然現在都是由小到大續步找尋更大的質數,所以:
當 Pm=已知最大質數,要知道 Pm+2是否質數,只需設 Y=((Pm+2)-3)/2=(Pm-1)/2,無論 Y是單數還是雙數,只要比較數據庫, 任何 Y-3n是否 (1+2n)的倍數都可以知道,根本不用每次都慢慢測試逐個計,而且最多只需比較數據庫中大約細過 Pm平方根的 n 便可,如此類推.
如此,便可不斷尋找更大的質數,方便快捷.其實只要Y=<Pm便可,亦即最大可以找尋 2Pm+3是否質數!
-----------
答案1:善用科技,用電腦.
答案2:比較數據庫,不需逐個計.
以證:只要肯思考,一定有解決方法.
結論:即使有決心,有恆心,都要肯思考先有用.
得分:Y=(P-3)/2
20200912