SDK - Self Destruction Kit

W tym dziale będę umieszczał moje drobne przemyślenia dotyczące studiów na Politechnice Wrocławskiej w ogólności, na wydziale Podstawowych Problemów Techniki (PPT) w szczególności.

Zanim zaczniemy wykład, chwila wprowadzenia. Zakładam, że znasz podstawowe oznaczenia w matematyce: f: Dziedzina -> Zbiór-wartości (funkcja), odwrócone A - "dla każdego", odwrócone E - "istnieje takie że", => - "jeżeli to".
Dla osób oglądających to na przykład w Linksie - sam używam :)))) : każdy obrazek ma opis starający się naśladować to, co obrazek oddaje, choć ze zrozumaiłych względów nie jest możliwe idealne odwzorowanie. Zatem oznaczenie in to "element należy do", zaw to podzbiór zbioru, a kwantyfikatory (odwrócone A i E) są nieodwrócone (chociaż znajdują się na początku każdego nawiasu, dla użatwienia rozpoznania). Koniec wstępu, zaczynamy.

Prawdy matematyczne

Weźmy następujące oznaczenia:
A - kosmos logiki matematycznej
- podkosmos kolokwiów kosmosu logiki
U - uniwersum studentów Politechniki Wrocławskiej
= ocena za kolokwium
= korbiastość zadań na kolokwium

Twierdzenie (o kolokwium dla grupy studentów)

Dowód: poprzez trywialne operacje empiryczne.

W tłumaczeniu: Dla każdej grupy studentów znajdzie się takie kolokwium, że żaden student nie zda

Przy powyższych oznaczeniach, dodając:
= zrozumienie przez studenta materiału z logiki
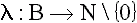= średnia długość zadania (w znakach)
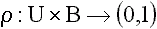= średnie prawdopodobieństwo rozwiązania zadania

otrzymujemy następujące twierdzenie o szerokim zastosowaniu dydaktycznym:

Pierwsza zasada studencka

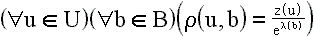
W tłumaczeniu: średnie prawdopodobieństwo rozwiązania zadania przez studenta rośnie liniowo wraz ze wzrostem zrozumienia materiału i maleje wykładniczo wraz ze wzrostem długości zadania

Druga zasada studencka (zasada szacowania oceny)

Rozbieżność pomiędzy ocenami własną studenta i sprawdzającego jego kolokwium jest wprost proporcjonalna do pewności siebie studenta i odwrotnie proporcjonalna do rozgarnięcia sprawdzającego.

Zasada łatwiejszych zadań

Lista zadań dowolnej grupy równoległej jest łatwiejsza od listy, którą student właśnie otrzymał.

Zasada malejącej wiedzy

Zrozumienie partii materiału przez studenta jest wprost proporcjonalne do iloczynu logarytmu dwójkowego z jego zdolności w danej dziedzinie i kwadratu czasu od terminu najbliższego kolokwium.

W tłumaczeniu: im student zdolniejszy, tym lepiej rozumie materiał; im bliżej do kolokwium, tym student mniej wie

Twierdzenie (o trzech studentach)

Jeśli na kolokwium dwóch dowolnie wybranych studentów siedzi w otoczeniu epsilonowym odpowiednio dobieranym do pilnującego, a pomiędzy nimi znajduje się trzeci student, to jeśli oceny dwóch pierwszych dążą do tej jednej granicy, to ocena trzeciego również dąży do tej samej granicy.

Dowód: natychmiastowy wniosek z pobieżnego przejrzenia kolokwiów.

Reguła czasu oddania pracy (pochodna praw Murphy'ego)

Jeśli chcesz oszacować czas, jaki zajmie skończenie danego zadania (nauki materiału, zrobienie pracy na semestr, napisanie programu na zaliczenie), weź przewidywany czas ukończenia zadania i pomnóż go przez cztery. Wynik, który otrzymasz, jest w jednostkach dwa rzędy wyższych.

Reguła dowodzenia twierdzeń

Jeśli przy w dowodzie twierdzenia wychodzą bzdury, należy założyć niewprost, że teza jest fałszywa i powtórzyć rozumowanie, które doprowadziło do bzdur. Na zakończenie należy napisać Wychodzą bzdury, więc założenie jest fałszywe. Zatem teza początkowa musi być prawdziwa.
(autor: Mikołaj Bartnicki)

Reguła zdarzeń pożądanych (pochodna praw Murphy'ego)

Prawdopodobieństwo zajścia jakiegoś zdarzenia jest odwrotnie proporcjonalne do stopnia, w jakim to zdarzenie jest pożądane.

W tłumaczeniu: im zdarzenie bardziej pożądane, tym mniej prawdopodobne

Twierdzenie (o ilości rozwiązań zadania)

Ilość różnych rozwiązań zadania jest odwrotnie proporcjonalna do zrozumiałości zadania i wprost proporcjonalna do ilości studentów to zadanie rozwiązujących.

Dowód: poprzez sporządzenie dostatecznie niejasnej listy zadań

Fakt [fm1]

Ilość interpretacji zadania jest równa n!, gdzie n jest ilością symboli użytych do sformułowania zadania

Dowód: prosta ankieta wśród rozwiązujących zadania z dowodu poprzedniego twierdzenia.

Twierdzenie (o komplikacji formuł)

Niech: F - zbiór formuł
V - zbiór zmiennych stosowalnych w zdaniach
C - zbiór spójników logicznych
Q - zbiór kwantyfikatorów
- zrozumiałość formuły
- modyfikacja formuły (dodanie zmiennej, kwantyfikatora lub spójnika)
Wtedy:


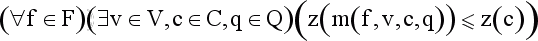
Dowód: powyższa formuła

W tłumaczeniu: każdą formułę da się skomplikować przez wprowadzenie odpowiedniej ilości symboli logicznych

Definicja [df1]

Wykładem nazywamy proces przekazywania notatek prowadzącego do zeszytu słuchacza (zeszytów słuchaczy) bez udziału mózgu.
(poznane od EpoCa na IRCu)

Prawdy informatyczne

Podstawowa prawda Informatyki

Jeśli nauczysz się wszystkich możliwych wyjątków, z prawdopodobieństwem 1.20 zapomnisz, do jakich reguł się one stosowały. (ściągnięte z klienta e-mail Mozilli)

Fakt [fi1]

Zbiór funkcji w C/C++ i unarny operator * (dereferencja, wyjęcie spod wskaźnika) tworzą grupę cykliczną.
(fakt rozpowszechniany na licencji GNU/GPL, autor: Tomek Gołębiowski)

Fakt [fi2]

Każdy algorytm o złożoności obliczeniowej O(n)=k(n) (k - funkcja) da się zapisać w rekurencyjnej postaci klasy co najmniej O(n)=(k(n))².
Dowód: lektura tego kodu źródłowego

Lemat [li1] (o rekurencyjności operacji)

Każda funkcja w C/C++ daje się wyrazić rekurencyjnie.

Dowód:
Przeprowadźmy indukcję po złożoności funkcji:

1. + - * / = if if-else switch for while do-while ++ -- ; dają się wyrazić rekurencyjnie (może kiedyś zamieszczę przykłady :] )
2. Oznaczmy przez __OPER__ dowolną operację elementarną z poprzedniego punktu. Niech f() daje się wyrazić rekurencyjnie. Wtedy f1(){__OPER__; f();} i f2(){f(); __OPER__;} również dają się przedstawić w postaci rekurencyjnej.

Twierdzenie (o implementacji algorytmu)

Każdy algorytm o złożoności obliczeniowej O(n)=k(n) (k - funkcja) da się zaimplementować w postaci rekurencyjnego programu o złożoności obliczeniowej co najmniej O(n)=(k(n))².

Dowód: Prosty wniosek z lematu [li1] i faktu [fi2]