| SELF |
78 |
S.B. Karavashkin, O.N. Karavashkina |

|
As a merit of
Magnus method we can mark, he did not follow the conventional way, introducing the
boundary conditions for an unfixed end, but suggested a complex way to get over the
discrepancy of solutions. ''We can now write the cited expression (13) for the amplitude Xp
as |
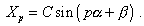
|
(42) |
The introduced constant  gives us the scope to 'adjust' the solution to
the boundary condition in the line beginning. The value gives us the scope to 'adjust' the solution to
the boundary condition in the line beginning. The value  makes it impossible, because when substituting
(42) into the amplitude relationship (9), we see that the relation between makes it impossible, because when substituting
(42) into the amplitude relationship (9), we see that the relation between  and and  is determined
by (16). The distinction from the previous item relation is, when studying the natural
vibrations, we have first to find is determined
by (16). The distinction from the previous item relation is, when studying the natural
vibrations, we have first to find  as a relative natural frequency, and vice versa, for the
forced vibrations the relative frequency of excitation as a relative natural frequency, and vice versa, for the
forced vibrations the relative frequency of excitation  is known'' [4, p.282]. On this grounds Magnus
has replaced the discrete relation between is known'' [4, p.282]. On this grounds Magnus
has replaced the discrete relation between  and and  (14) by the continuous relation (14) by the continuous relation  ( ( ). ).
Further, ''at the boundary condition given here, taking into
account (42), the following requirements are imposed on the amplitudes: |
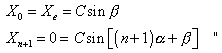
|
(43) |
[4, p.283]. The result is |
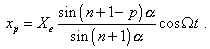
|
(44) |
To compare (44) with (37), note that Xe
corresponds to the amplitude of the first element (40), 0 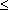 p p 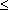 n +1, while 1 n +1, while 1 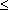 i i 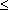 n . Noting
these features, on the basis of (37), we obtain n . Noting
these features, on the basis of (37), we obtain |

|
(45) |
Noting moreover that according to (16) and (19) |

|
(46) |
and substituting (45) into (37), we obtain |

|
(47) |
which fully corresponds to (44).
The demerits of Magnus method are seen from the consideration. If
lifting the fixation from the second end of a line, the condition (43) will be violated
and the whole method will not work. Besides, the Magnus method has established the
relationship between the vibration amplitudes of the pth and the first body, but
did not establish the relation between this body vibration and the external force
parameters. As we see from (45), this relationship is quite complex. Basically, this
demerit reflects the impossibility to specify vibrations exactly at the free end of a line
with the help of boundary conditions, since, as it follows from (45), this amplitude
vitally depends on the external force parameters. None the less, despite these demerits,
the Magnus method completely corroborates (37)-(39) validity in the particular case of a
finite line having one end free. And not only in the band of periodical regime. Basing on
(44), Magnus considered further also aperiodical (overcritical) regime. ''First of all we
see that for all frequencies  > 2 > 2 0, i.e. for all 0, i.e. for all  * = * =  - i - i , the signs before the amplification coefficients
alternate, so the chain masses always vibrate in anti-phase with the neighbouring masses''
[4, p.284]. ''It follows from the hyperbolic sine function behaviour that in the most
general case for each mass, with the growing , the signs before the amplification coefficients
alternate, so the chain masses always vibrate in anti-phase with the neighbouring masses''
[4, p.284]. ''It follows from the hyperbolic sine function behaviour that in the most
general case for each mass, with the growing  *, the more this mass is remote from the chain start the
more the amplification coefficient value decreases. For the last mass of a chain (p
= n) the amplification coefficient is *, the more this mass is remote from the chain start the
more the amplification coefficient value decreases. For the last mass of a chain (p
= n) the amplification coefficient is |
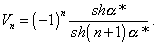
|
(48) |
At quite large n this function decreases so much with the
growing frequency that practically we can say, the frequency higher than that boundary is
cut off. The chain does not pass the frequencies  > 2 > 2 0, it works as a low-frequency
filter'' [4, p.285]. Blakemore [15] in his calculation also obtains the anti-phase
vibrations in critical regime for an infinite 1D crystalline lattice. But he considers
neither critical nor aperiodical regimes, thinking, due to the incompleteness of his
solutions, that the phase delay at the overcritical domain will exceed 0, it works as a low-frequency
filter'' [4, p.285]. Blakemore [15] in his calculation also obtains the anti-phase
vibrations in critical regime for an infinite 1D crystalline lattice. But he considers
neither critical nor aperiodical regimes, thinking, due to the incompleteness of his
solutions, that the phase delay at the overcritical domain will exceed  . And due to the strong
absorption, ''the waves having angular frequency exceeding . And due to the strong
absorption, ''the waves having angular frequency exceeding  m = 2v0
/ a cannot exist in an imaginary 1D crystal'' [15, p.110]. None the
less, in many problems of the applied mechanics, solid physics etc., not only the energy
transmission by an elastic line but also the process of energy accumulation and
redistribution within the line is important. The local accumulation and redistribution of
the vibration energy is inherent in the aperiodical regime. This is just the case when,
for example, under an external force the reaction at the support is absent, even under the
dynamical load in the excitation region being critical for the elastic constraints. This
is a very important aspect, when studying the fatigue processes in elastic systems. We
should note here, at the periodical regime the neighbouring elements vibrate in the
anti-phase - it means that the constraints are loaded maximally. In this view the case is
important when the external force acted on the line interior elements. With it both
supports will not experience the load, while in the excitation region the critical
vibrations can take place, crushing the internal constraints of an elastic line. And when
the external force "action radius" dependence on the frequency and elastic
system parameters is complicated, it is important to obtain the solutions of modelling
system equations in the analytical form. These indicate the most exactly the measure of
each factor effect and allow choosing qualitatively the elastic line parameters
dependently on the external force type. m = 2v0
/ a cannot exist in an imaginary 1D crystal'' [15, p.110]. None the
less, in many problems of the applied mechanics, solid physics etc., not only the energy
transmission by an elastic line but also the process of energy accumulation and
redistribution within the line is important. The local accumulation and redistribution of
the vibration energy is inherent in the aperiodical regime. This is just the case when,
for example, under an external force the reaction at the support is absent, even under the
dynamical load in the excitation region being critical for the elastic constraints. This
is a very important aspect, when studying the fatigue processes in elastic systems. We
should note here, at the periodical regime the neighbouring elements vibrate in the
anti-phase - it means that the constraints are loaded maximally. In this view the case is
important when the external force acted on the line interior elements. With it both
supports will not experience the load, while in the excitation region the critical
vibrations can take place, crushing the internal constraints of an elastic line. And when
the external force "action radius" dependence on the frequency and elastic
system parameters is complicated, it is important to obtain the solutions of modelling
system equations in the analytical form. These indicate the most exactly the measure of
each factor effect and allow choosing qualitatively the elastic line parameters
dependently on the external force type. |