|






| |
4 - MASS IN OUR RELATIVITY
( 4.1 ) In this section we shall
derive the measured mass of the moving train relative to the static observer.
Now, suppose a static observer on the earth surface, also a static train which
inside it a static rider and clock. Then, both the rider and the observer are
agreeed at the time 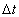 = 0, where at
this time the velocity of the train was equal to zero. = 0, where at
this time the velocity of the train was equal to zero.
Now, at 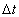  0
the train moved with constant velocity 0
the train moved with constant velocity 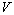 . after the train
had travelled the distance . after the train
had travelled the distance 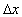 relative to the static
observer, it stopped. In this case, the static observer registered the time relative to the static
observer, it stopped. In this case, the static observer registered the time 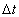 according to his clock to the train to travel the distance
according to his clock to the train to travel the distance 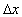 .
Then, he secured the velocity of the train was .
Then, he secured the velocity of the train was 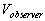 , where , where
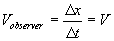
Then, the measured momentum of the
train relative to the observer was
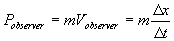 ( 4.1.1 ) ( 4.1.1 )
Where
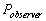 is the measured momentum for the
static observer when the train was moving. is the measured momentum for the
static observer when the train was moving.
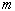
is
the measured mass for the static observer when the train was moving.
For the rider of the train, when the train stopped, the
measured distance that the train is travelled for the rider would be 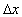 [ as we have seen in ( 3.4 ) ], but he would secure, this distance was travelled
at the time
[ as we have seen in ( 3.4 ) ], but he would secure, this distance was travelled
at the time 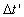 according to his clock, where according to his clock, where
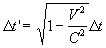
Where, 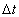 is the
time measured by the static observer. is the
time measured by the static observer.
Thus, the rider would secure, the velocity of his train was 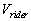 ,
where ,
where
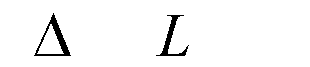 ( 4.1.2 ) ( 4.1.2 )
We see equation ( 4.1.2 ) is in contrast
with equation ( 3.1.1 ), where in equation ( 3.1.1 ) 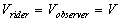 ,
but in equation ( 4.1.2 ) ,
but in equation ( 4.1.2 )
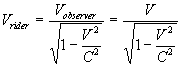 , ,
that is because, equation ( 3.1.1 ) is
just applied during the motion of the train of the rider, where in this case the
measured distance that the train travels during the motion for the rider is 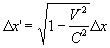 ,
where ,
where  is the measured distance that the train travels
for the static observer. when the train stops, then is the measured distance that the train travels
for the static observer. when the train stops, then  , [
as we have seen in figure ( 3.4.1 ) ]. , [
as we have seen in figure ( 3.4.1 ) ].
Thus, the measured momentum of the
train relative to the rider ( according to his clock ) was 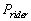 ,
where ,
where
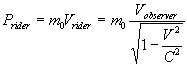 ( 4.1.3 ) ( 4.1.3 ) 
Where, 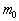 is the rest mass of
the train, where we proposed the measured mass of the moving train for the rider
is the rest mass. If we proposed both, the rider and the observer will be agreed
at the measured momentum, then by equalizing equations ( 4.1.1 ) and ( 4.1.3 )
we get is the rest mass of
the train, where we proposed the measured mass of the moving train for the rider
is the rest mass. If we proposed both, the rider and the observer will be agreed
at the measured momentum, then by equalizing equations ( 4.1.1 ) and ( 4.1.3 )
we get
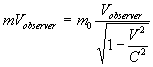

Then
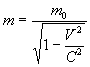 ( 4.1.4 ) ( 4.1.4 )
Equation ( 4.1.4 ) represents the relativistic mass of the
moving train for the static observer.
( 4.2 ) Now, suppose the rider of
the moving train B desire measuring the mass of the static train A during his
train motion. As we have seen, the rider will secure, the time that is measured
by his clock is equal to the time that is measured by the clock of the static
train, where  , where , where 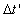 is the
time that is measured by the clock of the rider for himself, and is the
time that is measured by the clock of the rider for himself, and 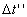 is the time that is measured by the clock of the static train A for the rider.
Now, if train B travelled the distance
is the time that is measured by the clock of the static train A for the rider.
Now, if train B travelled the distance 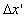 for the rider,
then, it is also considered for the rider that train A is travelled the distance for the rider,
then, it is also considered for the rider that train A is travelled the distance
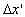 , where it is considered for the rider, train A is
moving with velocity , where it is considered for the rider, train A is
moving with velocity 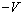 , where , where 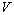 is the velocity of train B. Thus, the measured momentum of train A for the rider
( according to his clock ) is
is the velocity of train B. Thus, the measured momentum of train A for the rider
( according to his clock ) is 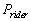 where
where
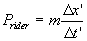 ( 4.2.1 ) ( 4.2.1 )
The measured momentum of train A
for itself relative to the reference frame of the moving train B ( according to
the clock of train A for the rider ) is 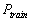 ,
where ,
where
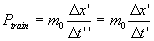 ( 4.2.2 ) ( 4.2.2 )
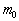 is the rest
mass of the train. is the rest
mass of the train.
If we equalized equations ( 4.2.1 ) and ( 4.2.2 ), we get
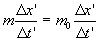
From that we get
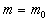 ( 4.2.3 ) ( 4.2.3 )
Thus we get, the rider of the moving train B will
measure the mass of the static train A equals to the rest mass of it as for a
static observer on the earth surface.
( 4.3 ) Now, suppose train A started at rest to move with
constant velocity 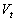 , and after it
had travelled the distance , and after it
had travelled the distance 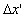 for the rider of the moving
train B, it stopped. In this case, the rider secured, train A travelled the
distance for the rider of the moving
train B, it stopped. In this case, the rider secured, train A travelled the
distance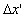 in a time separation in a time separation 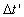 according to his clock, then its measured velocity for him was
according to his clock, then its measured velocity for him was 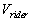 ,
where ,
where
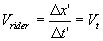
And then the measured momentum is 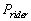 ,
where ,
where
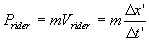 ( 4.3.1 ) ( 4.3.1 )
Where 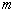 is the measured
momentum of the moving train A for the rider of the moving train B. is the measured
momentum of the moving train A for the rider of the moving train B.
According to the clock of the moving train A for the rider, this distance was
travelled at a time 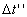 where where
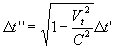
Then the velocity of train A for itself relative to the reference frame of
the moving train B is 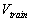 , where , where
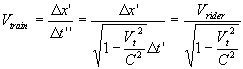
Thus its momentum for itself for the reference frame of the rider of the
moving train B is 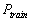 , where , where
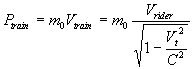 ( 4.3.2 ) ( 4.3.2 )
If we equalize equations ( 4.3.1 ) and ( 4.3.2 ), we get
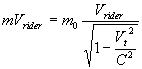
Thus we get
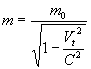 ( 4.3.3 ) ( 4.3.3 )
Equation ( 4.3.3 ) represents the measured mass of the moving
train A for the rider of the moving train B ( relativistic mass ), where
according to the equation, the mass is increased during the motion. For an
observer static on the earth surface, the relativistic mass of the moving train
A is given also as in equation ( 4.3.3 ), where both the rider and the observer
will measure the velocity 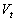 and
rest mass and
rest mass 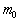 , and from that we see,
the motion of the train of the rider does not affect to his calculations
comparing to the calculations of the static observer on the earth surface, where
both will get the same calculations, but, the motion of the train of the rider
makes him to get these calculations slower than the observer. , and from that we see,
the motion of the train of the rider does not affect to his calculations
comparing to the calculations of the static observer on the earth surface, where
both will get the same calculations, but, the motion of the train of the rider
makes him to get these calculations slower than the observer.
5 - EQUIVELANCE OF MASS AND ENERGY
( 5.1 ) The kinetic energy of train
A for a static observer on the earth surface or a rider of the moving train B is
given by calculating the work done in increasing its speed from zero to 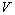 .
Suppose the force .
Suppose the force 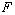 acts parallel
to the distance acts parallel
to the distance 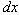 of train A, then
the work of train A, then
the work 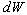 done on it is given by done on it is given by
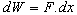
Newton’s second law is expressed
by
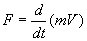
Thus
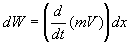
Since 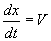 , then
we get , then
we get
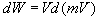
As we have seen previously, the measured mass of train A for the observer and
the rider is 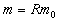 , then we get , then we get
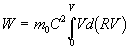
By integrating the equation above we get
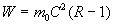
Since the work  is done to
increase the velocity of train A from zero to is done to
increase the velocity of train A from zero to 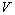 ,
then it produced a changing in its kinetic energy from zero to ,
then it produced a changing in its kinetic energy from zero to 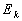 ,
thus ,
thus
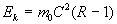 ( 5.1.1 ) ( 5.1.1 )
Equation ( 5.1.1 ) represents the kinetic energy 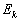 of the moving train A for the observer or the rider. We can write equation (
5.1.2 ) as
of the moving train A for the observer or the rider. We can write equation (
5.1.2 ) as
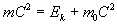 ( 5.1.2 ) ( 5.1.2 )
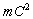 is the total energy of train
A. is the total energy of train
A.
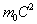 is the rest mass energy of train A. is the rest mass energy of train A.
Thus, we can express the total energy 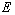 of any particle for any frame of reference as
of any particle for any frame of reference as
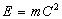 ( 5.1.3 ) ( 5.1.3 )
Equation ( 5.1.3 ) leads to the equivalence of mass and
energy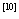 , where according to this
equation we conclude the mass and energy are two faces for one currency. , where according to this
equation we conclude the mass and energy are two faces for one currency.
6 - ENERGY IN OUR RELATIVITY
( 6.1 ) As we know from the Quantum
theory, the energy is considered as photons, have a rest mass equals to zero,
and we can express the energy that is held by any photon is given by the
equation
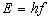 ( 6.1.1 ) ( 6.1.1 )
Where, 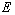 is the
energy that is held by the photon, is the
energy that is held by the photon, 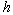 is Plank’s constant, and
is Plank’s constant, and 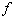 is
the frequancy of the wave of the photon. is
the frequancy of the wave of the photon.
According to the concept of equivalence of mass and energy,
the equivalent mass 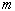 of any
photon is given by of any
photon is given by
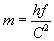 ( 6.1.2 ) ( 6.1.2 )
Now, suppose a train moving with constant velocity 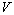 and a static observer on the earth surface. As we know, the motion of the clock
inside the train is slower than on the the earth surface for the static
observer, where, the time that is measured by the observer is
and a static observer on the earth surface. As we know, the motion of the clock
inside the train is slower than on the the earth surface for the static
observer, where, the time that is measured by the observer is 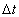 via his clock, and
via his clock, and 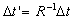 via the clock
of the moving train. Since the frequency of a wave is defined as the number of
cycles at the unit of time, thus, the frequency via the clock
of the moving train. Since the frequency of a wave is defined as the number of
cycles at the unit of time, thus, the frequency 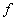 of
any wave on the earth surface for any observer static on the earth surface is
given by of
any wave on the earth surface for any observer static on the earth surface is
given by
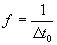 ( 6.1.3 ) ( 6.1.3 )
Now, suppose this wave entered inside the moving train, then
the frequency 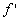 of the wave will be as of the wave will be as
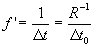
Thus
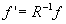 ( 6.1.4 ) ( 6.1.4 )
Where, from equation ( 6.1.4 ), the frequency of the wave
will be less inside the moving train than outside for the static observer. Thus,
the energy 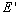 that is held by any
photon inside the moving train is given by that is held by any
photon inside the moving train is given by
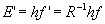
Thus from equation ( 6.1.1 ) we get
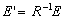 ( 6.1.5 ) ( 6.1.5 )
Equation ( 6.1.5 ) represents the endured energy inside the
moving train for the reference frame of the static observer on the earth
surface. The difference of energy 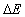 of the reference
frame of the earth surface and the moving train is given by of the reference
frame of the earth surface and the moving train is given by
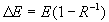 ( 6.1.6 ) ( 6.1.6 )
Back |