|






| |
RELATIVITY IN QUANTUM
Azzam K.I. AlMosallami
Arab Consultants Group, P.O. Box 1067
Gaza, Palestine, Via Israel
Abstract
The concepts, principles and laws on which Einstein built his
relativity theory (special and general) is in contrast with the concepts,
principles and laws on which the quantum theory is built.
The goal of our work is to get a new thoery that agrees with
the concepts, principles and laws of quantum and contains all the experimental
measurements of the relativity. On other words, deriving the equations of the
relativity which agree with the experimental measurements on the basis of the
concepts, principles and laws of quantum (Copenhagen School).
In part 2, section 1, I derive a new formula for Newtonís
second law, it expresses a quantized force, and agrees with the concepts,
principle, and laws of quantum. In section 2, I also derive the quantized
inertial force.
Introduction
When Einstein started building his special relativity theory,
he was believed in the objective existance of the phenomenon, where we can find
that in the derivation of equations of the relativity. Also, he was believed in
the continuity principle and in the causality and determinism laws in the world.
Quantum theory discovered the observer has the main formation
of the phenomenon, and that is clear in the definition of Heisenberg to the wave
function (1958), where he defined it as " it is a mixture between two
things, the first is the reality, and the second is our realizing to this
reality."
Einstein was disagreed with this concept to the phenomenon,
where Pais said (1979), when he was walking with Einstein, he said " look
at the moon, do you believe it is existed because we are looking at it.
Also, quantum theory fosters the discontinuity principle,
uncausality and indeterminism laws in the world.
The mathmatical formation of the relativity depends on
Riemanís space with four dimensions, but quantum on Hilbert space with
infinite dimensions.
Stapp said (1972) " The Copenhagen School refused
understanding the world as the concepts of (space-time), where it considers the
relativity theory is inconsistant for understanding the micro world, where
quantum theory is formed the basis for understanding this word."
In equations of relativity of Einstein, it can be measured
the velocity of a particle and its location at the same time, but the
experimental measurements proved contrary of that ( Heisenberg uncertainty
principle )
Oppenheimer said " Einstein -in his last years
researching- tried proving the inconsistancy of the laws of quantum theory but
he failled. After all that Einstein said, he dislikes the quantum theory,
especially Heisenberg uncertainty principle."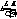
In our work, we define the reference frame as the frame at
which the observer is static, and the inertial frame is that frame which its
velocity is constant with time for any inertial frame of reference.
 THEOERY THEOERY
1- POSTULATES OF THE THEORY
1- The speed of light is constant and equals to 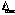 in any inertial frame of reference , where
in any inertial frame of reference , where 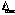 is the speed of light in vacuum.
is the speed of light in vacuum.
2- The speed of light in any frame moving with constant velocity 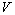 is
equal to is
equal to 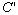 for any inertial frame
of reference, where for any inertial frame
of reference, where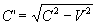 , whereas , whereas 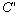 does not depend on the direction of the velocity of the moving frame, it depends
only on the absolute value of the velocity.
does not depend on the direction of the velocity of the moving frame, it depends
only on the absolute value of the velocity.
To understand the two potulates, suppose a static observer on
the earth surface, in this case the earth surface is considered as a reference
frame. If the static observer made an experiment for measuring the speed of
light in his reference frame he would find it equals to 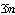 .
Also, if there is a train moving with constant velocity .
Also, if there is a train moving with constant velocity 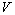 on the earth surface, and one of the static riders of it made an experiment for
measuring the speed of light inside his train, in this case the moving train is
considered as a reference frame, thus the speed of light that the rider would
measure equals to
on the earth surface, and one of the static riders of it made an experiment for
measuring the speed of light inside his train, in this case the moving train is
considered as a reference frame, thus the speed of light that the rider would
measure equals to  , as for the
static observer , and this is what the first postulate includes. , as for the
static observer , and this is what the first postulate includes.
Now, suppose the static observer made an experiment for
measuring the speed of light inside the moving train, in this case he would find
it equals to 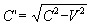 , and this is what
the second postulate includes. Now If , and this is what
the second postulate includes. Now If 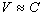 then
then 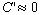 , that means in quantum the
wave function , that means in quantum the
wave function 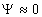 , thus, the probability of getting any
information inside the train for the observer approaches zero, where , thus, the probability of getting any
information inside the train for the observer approaches zero, where 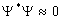 ,
where ,
where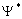 is the complex conjugate of is the complex conjugate of
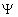 . .
2-TIME IN OUR RELATIVITY
( 2.1 ) Suppose a train at rest and a static
observer , on the earth surface. The length of the train is 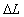 .
If one of the riders of the train sent a ray of light along the length the
train. Thus the time required to the ray of light to pass the length of the
train for the static observer and the rider is .
If one of the riders of the train sent a ray of light along the length the
train. Thus the time required to the ray of light to pass the length of the
train for the static observer and the rider is 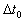 ,where ,where
 ( 2.1.1 ) ( 2.1.1 ) 
Now, suppose the train moved with constant velocity 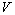 and then the rider sent a ray of light along the length of his train during the
motion. If the static observer catches his clock and desired computing the time
required to the ray of light to pass the length of the moving train. According
to the second postulate, the speed of light inside the moving train is
and then the rider sent a ray of light along the length of his train during the
motion. If the static observer catches his clock and desired computing the time
required to the ray of light to pass the length of the moving train. According
to the second postulate, the speed of light inside the moving train is 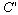 relative to the static observer, where
relative to the static observer, where 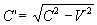 . Thus the time
required to the ray of light to pass the length of the moving train is . Thus the time
required to the ray of light to pass the length of the moving train is 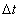 for the observer, where
for the observer, where
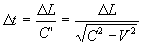
From the second postulate, we proposed, 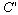 does not depend on the direction of transmitting the ray of light comparing to
the direction of the velocity of the train. Also, the equation above is in
contrast with the Lorentz transformation equations. Lorentz transformation
equations built on the concepts of continuity, causality, and determinism, but,
in our work we believe in the discontinuity, uncausality and indeterminism. The
measurement that is taken in the equation above is taken from a wave function,
and to get another measurement we must get another wave function ... , and vise
versa and those wave functions are unrelated. Also, Lorentz transfomation
equations proposed that we can measure the velocity of the train and its
location at the same time, and that is in contrast with the uncertainty
principle of Heisenberg.
does not depend on the direction of transmitting the ray of light comparing to
the direction of the velocity of the train. Also, the equation above is in
contrast with the Lorentz transformation equations. Lorentz transformation
equations built on the concepts of continuity, causality, and determinism, but,
in our work we believe in the discontinuity, uncausality and indeterminism. The
measurement that is taken in the equation above is taken from a wave function,
and to get another measurement we must get another wave function ... , and vise
versa and those wave functions are unrelated. Also, Lorentz transfomation
equations proposed that we can measure the velocity of the train and its
location at the same time, and that is in contrast with the uncertainty
principle of Heisenberg.
From equation ( 2.1.1 ), we get
 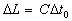
Then
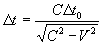
Thus
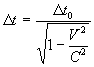 ( 2.1.2 ) ( 2.1.2 )
Where  is the time required to the
ray of light to pass the length of the train when it is at rest. is the time required to the
ray of light to pass the length of the train when it is at rest.
In the derivation of equation ( 2.1.2 ) we considered the
static observer on the earth surface will measure the length of the moving train
equals to 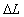 as it is at rest, and that is in contrast with
the length contraction of Einstein. as it is at rest, and that is in contrast with
the length contraction of Einstein.
Equation ( 2.1.2 ) means, the time separation of any event
that happens in any moving frame with constant velocity 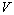 is bigger than the rest time separation, (if the same event happens when the
frame at rest) for any frame of reference.
is bigger than the rest time separation, (if the same event happens when the
frame at rest) for any frame of reference.
( 2.2 ) Now, suppose one of the riders of the
moving train catches his clock inside the train and he desires measuring the
time required to the ray of light to pass the length of his train during the
motion. According to equation ( 2.1.2 ), the time separation for any event which
happens inside the train is bigger when it is moving than when it is at rest for
the reference frame of the earth surface. And because the motion of the clock is
an event inside the train, thus its movement will be slower when the train is
moving than when it is at rest for the reference frame of the earth surface.
Thus, the clock of the rider will be slower than the clock of the static
observer. And, if we assumed, both the observer and the rider will agree on the
beginning of the event and ending it inside the moving train, thus, if the
observer computes by his clock the time 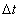 for the ray of light to pass the length of the moving train, then the rider will
compute the time
for the ray of light to pass the length of the moving train, then the rider will
compute the time 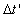 , where , where
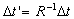
Where
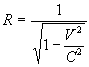 
Since from equation ( 2.1.2 )
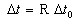
Thus we get
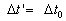
Thus, we can write equation ( 2.1.2 ) as
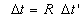 ( 2.2.1 ) ( 2.2.1 )
According to equation ( 2.2.1 ), the speed of light for the
moving rider according to his clock is 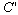 ,
where ,
where
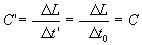 ( 2.2.2 ) ( 2.2.2 )
Equation ( 2.2.1 ) leads us to the first postulate of the
theory, the slowing of the speed of light for any frame moving with constant
velocity 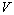 , leads to slowing of time in that frame
(movement of clocks). Thus, the speed of light for all frames of reference is
the same and equals to C. , leads to slowing of time in that frame
(movement of clocks). Thus, the speed of light for all frames of reference is
the same and equals to C.
Thus, in this case we have
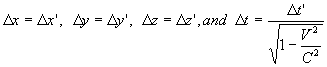 . .
( 2.3 ) Suppose the static
observer desires comparing the motion of clock of the moving rider with the
motion of his clock. According to equation ( 2.1.2 ), and, because the motion of
the clock of the rider is an event inside the moving train, thus, the clock will
be slower when the train is moving than when it is at rest for the observer.
Thus, if the observer looks at his clock and computes the time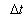 ,
in this moment he will find that, the clock of the rider computes the time ,
in this moment he will find that, the clock of the rider computes the time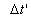 where
where
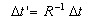
( 2.4 ) Now, suppose the rider of the moving train
desires using the clock of the static observer for computing the time required
to the ray of light to pass the length of his train. The time which will be
measured by the static observer via his clock is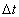 where
where
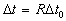
If we consider the rider is moving with constant velocity to
the right, then the clock of the observer is moving with the same velocity to
the left relative to the rider, in this case, the riderís frame is considered
as a reference frame and the clock as a frame moving with constant velocity 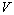 for him. Thus, according to the preceding discussion, the clock will be slower
for the rider than the observer for the reference frame of the earth surface.
Thus, if the observer computes the time
for him. Thus, according to the preceding discussion, the clock will be slower
for the rider than the observer for the reference frame of the earth surface.
Thus, if the observer computes the time 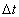 by his clock, in this moment the rider will compute the time
by his clock, in this moment the rider will compute the time 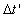 by the same clock [ or by his clock inside the train as we have seen in ( 2.2 )
], where
by the same clock [ or by his clock inside the train as we have seen in ( 2.2 )
], where
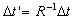
Suppose, the length of the train is 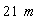 ,
and its speed is ,
and its speed is 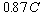 . If the clock
computes by . If the clock
computes by 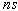 where where 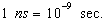 ,
then the time required to the ray of light to pass the length of the moving
train for the static observer is ,
then the time required to the ray of light to pass the length of the moving
train for the static observer is 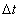 ,
where ,
where
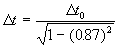
And
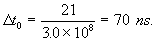
Then
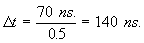 
Thus, the static observer will compute 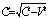 via his clock for the ray of light to pass the length of the moving train. For
the rider, the time is
via his clock for the ray of light to pass the length of the moving train. For
the rider, the time is 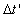 where where
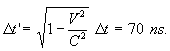
So, the rider will compute 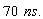 for the ray of light to pass the length of his train. Both, the observer and the
rider will agree on the beginning of the event and ending it, and when both used
the same clock to compute the time separation to this event , the clock was
slower for the rider than the observer. So, when the observer received
for the ray of light to pass the length of his train. Both, the observer and the
rider will agree on the beginning of the event and ending it, and when both used
the same clock to compute the time separation to this event , the clock was
slower for the rider than the observer. So, when the observer received 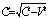 to the time separation, in this moment the rider received only the first
to the time separation, in this moment the rider received only the first 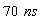 of the clock, where we can consider the rider lives in the past of the oberver
of the earth surface.
of the clock, where we can consider the rider lives in the past of the oberver
of the earth surface.
In this example we find when both the rider and the observer
used the same clock each one creates his clock to get his reading, and that is
in contrast with the objective existance of the phenomenon, where in our example
we obtain, the observer has the main formation of the phenomenon as in
Copenhagen School concepts.
( 2.5 ) Now, suppose train A at rest, its length
is 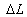 , also there are train B
moving with constant velocity , also there are train B
moving with constant velocity 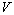 and a static observer on
the earth surface. Now, both the static observer and the rider of train B will
measure the time required to the ray of light to pass the length of the static
train A. For the observer, the measured time according to his clock is and a static observer on
the earth surface. Now, both the static observer and the rider of train B will
measure the time required to the ray of light to pass the length of the static
train A. For the observer, the measured time according to his clock is where
where
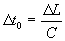
For the rider of train B, since train A is moving with
constant velocity -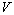 , thus the speed of light inside it
comparing to the reference frame of the static observer is , thus the speed of light inside it
comparing to the reference frame of the static observer is 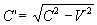 ,
thus the rider should been computing the time ,
thus the rider should been computing the time 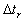 for the
event where for the
event where
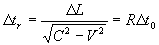
Where,  is the time separation of the
event when the train of the rider is static. is the time separation of the
event when the train of the rider is static.
Because the riderís clock is slow during the motion for the
reference frame of the earth surface [ as we have seen in ( 2.2 ) ], thus, the
rider will compute the time 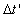 , where , where
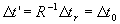 ( 2.5.1 ) ( 2.5.1 )
Equation ( 2.5.1 ) means, both the rider of the moving train
B and the static observer will measure the same time separation to the ray of
light to pass the length of the static train A, that leads us to, the measured
speed of light is the same for each one inside the static train A and it is
equal to 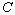 . Thus, we can write
equation ( 2.5.1 ) as . Thus, we can write
equation ( 2.5.1 ) as
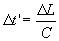
If both the static observer and the rider of the moving train
B agree with the time required to the ray of light to pass the length of the
static train A, then, they will be different in the beginning of the event and
ending it.
Let us assume both the observer and rider will agree on the
beginning of the event, in the condition of
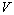 = 0 at = 0 at 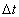 =
0 =
0
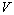 = 0.87C at = 0.87C at 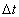 > 0
> 0
Where, at 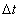 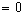 ,
before transmitting the ray of light, the velocity of train B of the rider was
equal to zero, and after transmitting the ray of light, the velocity of the
train was equal to 0.87C ( in this case, for simplicity we neglect the effect of
acceleration ) . In this condition, the static observer and the rider of the
moving train B will be agreed on the beginning of transmitting the ray of light
inside the static train A, and different in ending it. ,
before transmitting the ray of light, the velocity of train B of the rider was
equal to zero, and after transmitting the ray of light, the velocity of the
train was equal to 0.87C ( in this case, for simplicity we neglect the effect of
acceleration ) . In this condition, the static observer and the rider of the
moving train B will be agreed on the beginning of transmitting the ray of light
inside the static train A, and different in ending it.
If the length of the static train A is 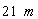 ,
thus, the time required to the ray of light to pass the length of the static
train A for the static observer is ,
thus, the time required to the ray of light to pass the length of the static
train A for the static observer is
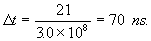
For the rider of the moving train B is from equation ( 2.2.2
)
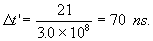
Because the time ( clock ) in the frame of the moving train B
is slower than the time ( clock ) of the static observer for the reference frame
of the earth surface, then, the ray of light will arrive to the end of the
static train A faster for the observer than the rider. Thus, if the observer
secures that, the ray of light arrived to the end of the train, in this moment
the rider secures that the ray of light arrived to the middle of the train.
Where, if the observer secures that the ray of light cut the distance 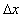 ,
in this moment the rider will secure that the ray of light cut the distance ,
in this moment the rider will secure that the ray of light cut the distance 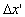 ,
where, ,
where, 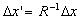 , also we get , also we get 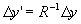 ,and ,and
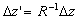 . Now, if the observer looks at
the clock of the rider, he will secure that the clock of the rider computes only . Now, if the observer looks at
the clock of the rider, he will secure that the clock of the rider computes only
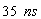 in the moment that his clock
computes in the moment that his clock
computes 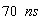 ,where ,where 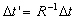 .
But, if the rider looks at the clock of the observer he will secure that the
clock of the observer computes only .
But, if the rider looks at the clock of the observer he will secure that the
clock of the observer computes only 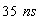 ,
as in his clock, while the observer secures that his clock computes ,
as in his clock, while the observer secures that his clock computes 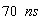 . .
( 2.6 ) Now, if the rider of the moving train
desires using the clock of the static observer in the condition of
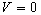 at at 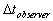  =
0 =
0
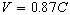 at 0 < at 0 <
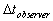 £ 4 sec. £ 4 sec.
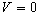 at at 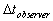 > 4 sec.
> 4 sec.
Where, 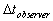 is the reading of the static
observer from his clock. is the reading of the static
observer from his clock.
We can draw 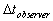 versus versus 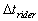 for the reference frame of the earth surface as in figure ( 2.6.1 ), where,
for the reference frame of the earth surface as in figure ( 2.6.1 ), where, 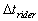 is the reading of the rider from the clock of the static observer.
is the reading of the rider from the clock of the static observer.
From figure ( 2.6.1 ), we find two straight lines, the first
for 0 < 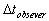 £
4 sec. , £
4 sec. ,
its slope = 0.5, and the second is for 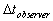 > 4 sec., its slope = 1
> 4 sec., its slope = 1
We find from the figure, the seconds between 2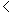 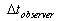 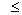 4
sec. would not be received by the rider, where, when the train of the rider
stopped at 4
sec. would not be received by the rider, where, when the train of the rider
stopped at 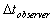  4 sec., he found that
the observer was reading the seconds at 4 sec., he found that
the observer was reading the seconds at 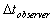 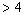 sec., while his last reading was equal to 2 sec. . That means, the events which
were done by the static observer between 2
sec., while his last reading was equal to 2 sec. . That means, the events which
were done by the static observer between 2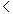  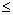 4
sec. were not be received for the rider of the moving train. 4
sec. were not be received for the rider of the moving train.
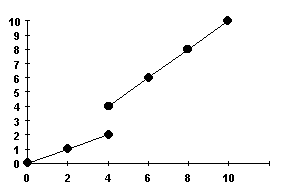  
Figure ( 2.6.1 ):  versus versus 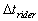 . .
From the figure we get, the observer has the main formation of the
phenomenon, where each one creates his clock during the motion, this is in
constrast with the objective existance of the phenomenon.
3 - THE VELOCITY IN OUR RELATIVITY
( 3.1 ) Now, letís go back to the
rider of moving train and the static observer, both, will make an experiment for
measuring the velocity of the moving train. They appointed two pylons and will
measure the time required for the train to pass the distance 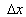 between the two pylons. Assume, both, will agree on the beginning of this event.
Now, the measured time by the static observer to the train to pass the distance
between the two pylons. Assume, both, will agree on the beginning of this event.
Now, the measured time by the static observer to the train to pass the distance 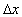 is
is 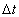 , according to his clock,
thus, the measured velocity for him is , according to his clock,
thus, the measured velocity for him is 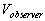 where where
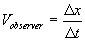
The equation above is not in
contrast with Heisenberg uncertainty principle, where 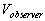 and
and 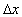 are not measured at the same
time, where when the observer measured the distance are not measured at the same
time, where when the observer measured the distance 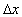 precisely for the train, he predicted by the equation above the velocity of the
train at the distance
precisely for the train, he predicted by the equation above the velocity of the
train at the distance 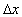 was equal to was equal to 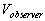 .
When the observer secures that the
train arrived to the second pylon, in this moment - during the motion - the
rider of the moving train does not secure that his train arrived to the second
pylon, where, he secures that the train is still arriving to the second pylon.
Now, if the static observer computes the time .
When the observer secures that the
train arrived to the second pylon, in this moment - during the motion - the
rider of the moving train does not secure that his train arrived to the second
pylon, where, he secures that the train is still arriving to the second pylon.
Now, if the static observer computes the time 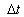 to the
train to arrive to the second pylon, in this moment the rider will compute the
time to the
train to arrive to the second pylon, in this moment the rider will compute the
time 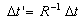 , also, if the observer
secures the train travels the distance , also, if the observer
secures the train travels the distance 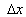 , in this moment
the rider will secure that his train travels the distance , in this moment
the rider will secure that his train travels the distance 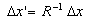 ,(
as we shall see in ( 3.4 ), figure ( 3.4.1 ) ). In this case, the measured
velocity of the moving train for the rider is ,(
as we shall see in ( 3.4 ), figure ( 3.4.1 ) ). In this case, the measured
velocity of the moving train for the rider is 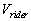 ,
where ,
where
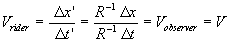 ( 3.1.1 ) ( 3.1.1 )
Thus, both the static observer and the rider of the
moving train will agree on the measured velocity of the moving train during the
motion and they will measure the real velocity 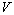 .
In Einsteinís special relativity,
the rider of the moving train will measure the distance between the two pylons
to be .
In Einsteinís special relativity,
the rider of the moving train will measure the distance between the two pylons
to be 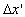 , where , where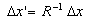 ,
where the distance between the two pylons will be contracted for the rider of
the moving train. That is because, Einstein was beleived in the objective
existance of the phenomenon, where according to this concept both the static
observer on the earth surface and the rider of the moving train will be agreed
that the train will start moving from the first pylon and then reaching to the
second pylon. Thus, according to the reciprocity principle of Einstein, the
observer of the earth surface will measure the length of the train to be ,
where the distance between the two pylons will be contracted for the rider of
the moving train. That is because, Einstein was beleived in the objective
existance of the phenomenon, where according to this concept both the static
observer on the earth surface and the rider of the moving train will be agreed
that the train will start moving from the first pylon and then reaching to the
second pylon. Thus, according to the reciprocity principle of Einstein, the
observer of the earth surface will measure the length of the train to be 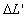 ,
where ,
where 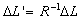 , where, the length of the
train will also be contracted for the observer. In our work, both the rider and
the observer will be agreed at the measured distance between the two pylons and
the length of the moving train, but, the motion makes the rider getting the
measurement slower than the observer. From that we refused the objective
existance of the phenomenon, and we foster the concept of Heisenberg to the wave
function that the observer has the main formation to the phenomenon. , where, the length of the
train will also be contracted for the observer. In our work, both the rider and
the observer will be agreed at the measured distance between the two pylons and
the length of the moving train, but, the motion makes the rider getting the
measurement slower than the observer. From that we refused the objective
existance of the phenomenon, and we foster the concept of Heisenberg to the wave
function that the observer has the main formation to the phenomenon.
( 3.2 ) Now, suppose another static
train A and inside it a static clock. Thus, as we have seen in ( 2.4 ) the rider
of the moving train B secures that the motion of the clock of the static train A
is analogous to his clock motion, where the time that he will measure it by his
clock is equal to the time that he will measure it by the clock of the static
train A. Also, the static observer secures that the motion of the clock of the
static train A is analogous to his clock motion. Now, if the train A moved with
constant velocity 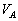 between the two pylons, then, as we
have seen in ( 3.1 ), both the rider of the moving train B and the static
observer will be agreed at the time separation for train A to pass the distance
between the two pylons, then, they will agree at the measured velocity of train
A, where each one will measure the velocity of the train equals to between the two pylons, then, as we
have seen in ( 3.1 ), both the rider of the moving train B and the static
observer will be agreed at the time separation for train A to pass the distance
between the two pylons, then, they will agree at the measured velocity of train
A, where each one will measure the velocity of the train equals to 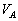 .
If a ray of light is sent along the length of the moving train A, then, the
measured time by the static observer for the ray of light to pass the length of
the train is .
If a ray of light is sent along the length of the moving train A, then, the
measured time by the static observer for the ray of light to pass the length of
the train is 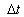 , where , where
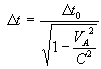
Also, the measured time by the rider of the moving
train B for the ray of light to pass the length of the moving train A is 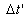 ,
where ,
where
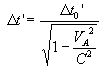
Where, 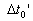 is
the measured time by the rider of the moving train B for the ray of light to
pass the length of train A when train A is static. is
the measured time by the rider of the moving train B for the ray of light to
pass the length of train A when train A is static.
Since, both, the static observer and the rider of the moving
train B are agreed at the time separation for the ray of light to pass the
length of train A when it is at rest as from equation ( 2.5.1 ), then we get
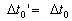
Thus
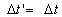
Thus, in this case, both the observer and the rider of the
moving train B will be agreed at the time separation for the ray of light to
pass the length of the moving train A, but, they will be differed in the
beginning and ending the event. Also, both, will agree that the clock of the
moving train A is slower than their clocks, also, they will be agreed at the
slowing rate of the clock.
In this example we have seen the motion of train B of the
rider did not affect to the calculations of the rider, where the calculations of
the rider were similar to the calculations of the static observer, but the
motion of train B made the rider to get these calculations slower than the
static observer.
( 3.3 ) Now, suppose a ball is
moving with constant velocity 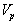 on the earth surface. The
rider of the moving train and the static observer will be agreed on the measured
velocity of the ball, where both will measure the velocity equals to on the earth surface. The
rider of the moving train and the static observer will be agreed on the measured
velocity of the ball, where both will measure the velocity equals to 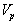 .
If this ball entered inside the moving train of the rider, then, the rider will
compute the time .
If this ball entered inside the moving train of the rider, then, the rider will
compute the time 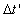 for the ball to pass the length for the ball to pass the length 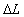 of his moving train, and the static observer will compute the time
of his moving train, and the static observer will compute the time 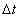 where
where 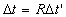 . Now, both the rider and the observer will agree
at the beginning of this event and ending it, but, they will be different in the
time separation of the event. In this case, the measured velocity of the ball
for the rider inside his moving train is . Now, both the rider and the observer will agree
at the beginning of this event and ending it, but, they will be different in the
time separation of the event. In this case, the measured velocity of the ball
for the rider inside his moving train is 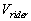 where
where
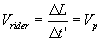
The equation above is not in
contrast with Heisenberg uncertainty principle, where 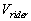 and
and 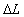 are not measured at the same time, where when the
rider measured the distance are not measured at the same time, where when the
rider measured the distance 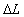 precisely, he predicted by
the equation above the velocity of the ball at precisely, he predicted by
the equation above the velocity of the ball at 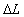 was
equal to was
equal to 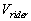 . .  And, the velocity of the moving
ball inside the moving train for the static observer is
And, the velocity of the moving
ball inside the moving train for the static observer is 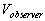 ,
where ,
where
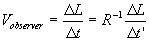
Thus
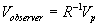 ( 3.3.1 ) ( 3.3.1 )
From equation ( 3.3.1 ), the motion
of the ball inside the moving train of the rider will be slower than outside for
the static observer and the measured velocity of the ball inside the train will
be less for the static observer than the rider.
( 3.4 ) Now, suppose the rider of the moving train and the static observer in
the condition of
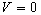 , , 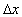 = 0 = 0
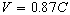 , 0 < , 0 <
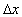 £ 10 £ 10 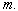
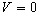 , , 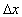 ≥
10 ≥
10 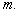 
This condition illustrates the
velocity of the moving train of the rider comparing to the distance 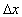 that is travelled by the train for the static observer. The graph of
that is travelled by the train for the static observer. The graph of 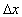 versus
versus 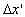 as in figure ( 3.4.1 ), where, as in figure ( 3.4.1 ), where, 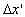 is the distance which is travelled by the train for the rider. From figure (
3.4.1 ), we find that, if the observer secures that the train travels
is the distance which is travelled by the train for the rider. From figure (
3.4.1 ), we find that, if the observer secures that the train travels 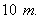 ,
the rider will secure that his train had just travelled the distance ,
the rider will secure that his train had just travelled the distance 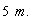 ,
and after that the train stopped. Now, if the rider disamouts from his train and
compues the distance that is passed by his train, he will find it equals to ,
and after that the train stopped. Now, if the rider disamouts from his train and
compues the distance that is passed by his train, he will find it equals to 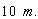 not
not 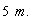 , and he will be taken aback,
that he transformed from , and he will be taken aback,
that he transformed from 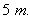 to to 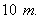 suddenly. Where he will be secured that the distance 5
suddenly. Where he will be secured that the distance 5   10 10
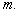 is not passed by his train, but
the static observer secures that the train passed this distance. is not passed by his train, but
the static observer secures that the train passed this distance.
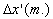
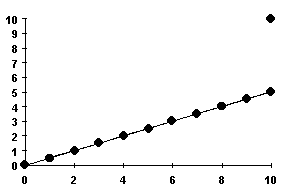 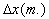
Figure ( 3.4.1 ): 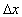 versus
versus 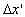 , the slope of the straight line is equal to 0.5. , the slope of the straight line is equal to 0.5.
Back Next |