
Quaternions
and more
complex numbers!
Let's start with: What is a quaternion?
It's a hypercomplex number!
It's a number in which the following relationships are satisfied.
i2
= j2 = k2 = ijk = − 1
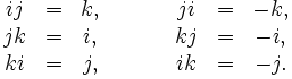
Brief history
In 1843, this guy called
Sir William Rowan Hamilton was taking a walk in Ireland. He was already
wondering how he could make complex numbers of greater dimensions, and while
he was taking this walk (on October 16) along the Royal Canal in Dublin, he
came up with the equation!

Quaternion plaque on Brougham (Broom)
Bridge, Dublin, which says:
Here as he walked by
on the 16th of October 1843
Sir William Rowan Hamilton
in a flash of genius discovered
the fundamental formula for quaternion multiplication
i2 = j2 = k2 = i j k = −1
& cut it on a stone of this bridge.
Quaternion Plaque
Properties
"The equation z2
+ 1 = 0, for instance, has the infinitely-many quaternion solutions
z = bi + cj + dk
with b2 + c2 +
d2 = 1. The conjugate
z * of the quaternion z =
a + bi + cj + dk is defined as
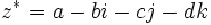
and the absolute value of z
is the non-negative real number defined by
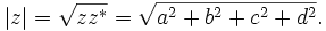 "
"
Quaternion
There's some more techno jargon, but that's al unimportant
and very confusing at this point.
4D Fractals
*Note: These are only 3D slices of the objects in 4
dimensional space.*







