Equação do Movimento para um Sietema Dinâmico Elementar

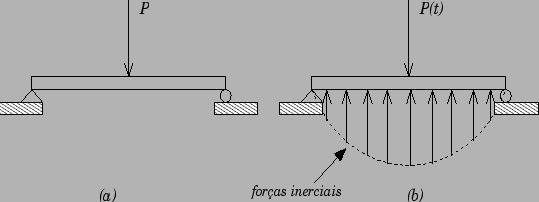A equação do movimento para um sistema dinâmico elementar é mais facilmente obtida a partir da aplicação direta do princípio de D'Alambert, expressando o equilíbrio de todas as forças que atuam no sistema. Assim como é mostrado na Figura 10.3 $b$ são quatro as forças que atuam na direção do grau de liberdade dinâmica: 1) A solicitação externa $P(t)$, 2) As forças inerciais $f_I$, 3) As forças de amortecimento $f_D$ e 4) As forças de mola $f_S$. A equação do movimento é simplesmente a expressão do equilíbrio dessas quatro forças, sendo escrita do seguinte modo:

$$f_I(t) + f_D(t) + f_S(t) = P(t)$$ (10.4)

Cada uma das forças do lado esquedo da Equação (10.4) é uma função do deslocamento $u(t)$, ou de alguma de suas derivadas.

De acordo com o princípio de D'Alambert, a força inercial é o produto da massa pela aceleração, assim:

$$f_I(t) = m \ddot{u} (t)$$ (10.5)

Assumindo a hipótese de que o amortecimento é viscoso, a força de amortecimento é proporcional a velocidade de acordo com a seguinte equação:

$$f_D(t) = c \, \dot{u} (t)$$ (10.6)

E finalmente, a força elástica é igual ao produto entre o deslocamento e a constante de mola, portanto:

$$f_S(t) = k u(t)$$ (10.7)

Quando substituimos as Equações (10.5 - 10.7) na Equação (10.4) temos a seguinte equação do movimento:

$$m \ddot{u} (t) + c \, \dot{u} + k u(t) = P(t)$$ (10.8)

Portanto, a Equação (10.8) é a equação do movimento para um sistema dinâmico elementar, obtida a partir da aplicação direta do princípio de D'Alambert.