As equações do movimento de qualquer sistema dinâmico representam expressões da segunda lei do moviemto de Newton, que diz que a taxa
de variação da quantidade de movimento de qualquer partícula de massa
 é igual a força que está agindo sobre essa partícula. Esta
relação pode ser matematicamente expressa pela seguinte equação diferencial:
é igual a força que está agindo sobre essa partícula. Esta
relação pode ser matematicamente expressa pela seguinte equação diferencial:
Onde
 é o vetor força aplicada e
é o vetor força aplicada e
![]() é o vetor posição da partícula de massa
é o vetor posição da partícula de massa
 . Felizmente, para a grande maioria dos problemas
de nosso interesse a massa do sistema permanece constante, o que nos leva a reescrever a Equação (10.1) do seguinte modo:
. Felizmente, para a grande maioria dos problemas
de nosso interesse a massa do sistema permanece constante, o que nos leva a reescrever a Equação (10.1) do seguinte modo:
Onde os dois pontos significam a derivada segunda em relação ao tempo. A Equação (10.2) indica que para os sistemas onde a massa
é constante em relação ao tempo, a força aplicada é igual ao produto da massa pela aceleração. Uma outra forma também usada para a mesma
equação é a seguinte:
Onde
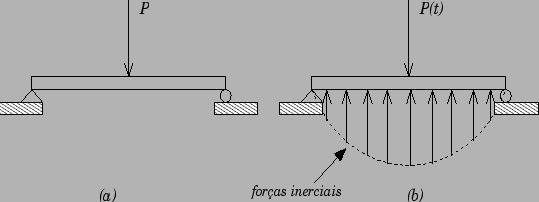
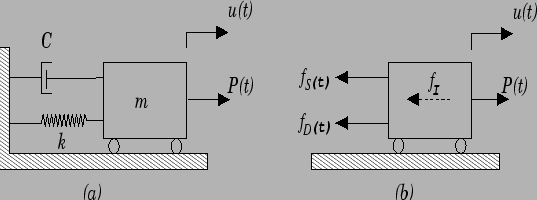 é chamado de força inercial de resistência a aceleração da massa. O conceito de que a aceleração da massa de
um sistema gera o surgimento de forças ierciais proporcionais a aceleração dos sistema é conhecido como o Princípio de D'Alambert. É uma
abordagem bastante conveniente em problemas de análise estrutural dinâmica porque permite que as equações do movimento sejam expressa na
formas de equações de equilíbrio dinâmico. Podem existir para a força
é chamado de força inercial de resistência a aceleração da massa. O conceito de que a aceleração da massa de
um sistema gera o surgimento de forças ierciais proporcionais a aceleração dos sistema é conhecido como o Princípio de D'Alambert. É uma
abordagem bastante conveniente em problemas de análise estrutural dinâmica porque permite que as equações do movimento sejam expressa na
formas de equações de equilíbrio dinâmico. Podem existir para a força
 diversas funções que expressem as mais variadas formas de
carregamento agindo em um sistema onde a massa pode ser concentrada. A forças elásticas que se opõe aos deslocamentos assim como também
as forças viscosas que se opõe as velocidades podem ser facilmente incluídas nessa formulação das equações do movimento, permitindo levar
em consideração a elasticidade dos corpos e o amortecimento do movimento. Para os problemas que estudaremos, esta abordagem para a obtenção
das equações do movimento se mostrará bastante conveniente, porém não devemos esquecer que existem outras abordagens mais convenientes
em outras situações, como pro exemplo, o princípio dos trabalhos virtuais, que também pode ser utilizado na formulação das equações do
movimento em sistemas dinâmicos mais complexos, envolvendo um grande número de graus de liberdade dinâmica.
diversas funções que expressem as mais variadas formas de
carregamento agindo em um sistema onde a massa pode ser concentrada. A forças elásticas que se opõe aos deslocamentos assim como também
as forças viscosas que se opõe as velocidades podem ser facilmente incluídas nessa formulação das equações do movimento, permitindo levar
em consideração a elasticidade dos corpos e o amortecimento do movimento. Para os problemas que estudaremos, esta abordagem para a obtenção
das equações do movimento se mostrará bastante conveniente, porém não devemos esquecer que existem outras abordagens mais convenientes
em outras situações, como pro exemplo, o princípio dos trabalhos virtuais, que também pode ser utilizado na formulação das equações do
movimento em sistemas dinâmicos mais complexos, envolvendo um grande número de graus de liberdade dinâmica.