Uma outra aplicação do método dos trabalhos virtuais é a determinação de forças incógnitas em alguns tipos de estruturas hiperestáticas. Nesses casos, o uso exclusivo das equações de equilíbrio é insuficiente para a solução do problema, uma vez que isso nos levaria a um sistema com mais incógnitas do que equações. A Figura 9.6 mostra um exemplo de estrutura hiperestática onde se deseja determinar as reações de apoio.
Na estrutura apresentada na Figura 9.6 os dois apoios do segundo gênero irão dar origem a quatro reações de apoio, e como só
existem 3 equações de equilíbrio disponíveis para o caso estudado, se usarmos apenas as equações de equilíbrio, teremos um sistema com
3 equações e 4 incógnitas. Vejamos então como resolver esse problema utilizando o método dos trabalhos virtuais.
Como a diferença entre incógnitas e equações de equilíbrio é de apenas 1, basta então determinar uma das reações de apoio incógnitas
para que se possa utilizar as equações de equilíbrio para determinar as outras três. Escolhemos então determinar o valor da reação
horizontal no apoio B, e para tal aplicaremos um deslocamento virtual conforme é mostrado na Figura 9.7
O deslocomento virtual imposto a estrutura fez com que surgizem os deslocamentos
![]() e
e
![]() nos respectivos pontos de
aplicação das forças
nos respectivos pontos de
aplicação das forças
![]() e
e
![]() . Como somente estas forças realizarão trabalho, a soma total do trabalho virtual devido ao deslocamento
virtual pode ser expressa por:
. Como somente estas forças realizarão trabalho, a soma total do trabalho virtual devido ao deslocamento
virtual pode ser expressa por:
Uma vez que o deslocamento
![]() está com o mesmo sentido da força
está com o mesmo sentido da força
![]() o trabalho virtual de
o trabalho virtual de
![]() será positivo. O mesmo não acontece
com o trabalho de
será positivo. O mesmo não acontece
com o trabalho de
![]() , uma vez que a força
, uma vez que a força
![]() tem sentido contrário ao deslocamento
tem sentido contrário ao deslocamento
![]() , e por esse motivo o trabalho de
, e por esse motivo o trabalho de
![]() terá
sinal negativo. Desse modo, podemos escrever que:
terá
sinal negativo. Desse modo, podemos escrever que:
Nos resta agora achar uma expressão que correlacione
![]() com
com
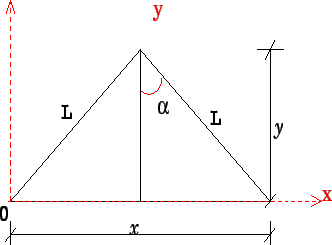
![]() . Para isso, posicionamos um sistema de eixos coordenados conforme
é mostrado na Figura 9.8.
. Para isso, posicionamos um sistema de eixos coordenados conforme
é mostrado na Figura 9.8.
Para o sistema de coordenadas apresentado na Figura 9.8 podemos escrever que:
Derivando ambas as expressões em relação a
![]() teremos que:
teremos que:
Uma vez que o sinal de cada parcela de trabalho já foi previamente definido, quando montou-se a equação da soma total dos trabalhos virtuais,
tomaremos agora, os valores das grandezas
![]() e
e
![]() , em módulo. Desse modo teremos que:
, em módulo. Desse modo teremos que:
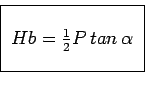
Podemos portanto expressar o valor da reção
![]() em função do ângulo
em função do ângulo
![]() e da força
e da força
![]() , do seguinte modo:
, do seguinte modo:
A grande maioria dos problemas que usam o método dos trabalhos virtuais para achar forças que equilibram mecanismos, ou reações em
sistemas hiperestáticos recai em uma equação do tipo
![]() , que na realidade é oriunda da expressão
em que a soma total de todos os trabalhos virtuais deve ser nula. Para resolver esse tipo de equação tem-se que achar um modo de relacionar
todos os
, que na realidade é oriunda da expressão
em que a soma total de todos os trabalhos virtuais deve ser nula. Para resolver esse tipo de equação tem-se que achar um modo de relacionar
todos os
![]() 's que aparecem na equação, de modo a expressar os trabalhos virtuais envolvidos em função de um único tipo de deslocamento.
Nos exemplos anteriores optou-se por exemplo em trocar os
's que aparecem na equação, de modo a expressar os trabalhos virtuais envolvidos em função de um único tipo de deslocamento.
Nos exemplos anteriores optou-se por exemplo em trocar os
![]() e
e
![]() envolvidos por um
envolvidos por um
![]() de modo que todos os
trabalhos virtuais envolvidos no problema ficassem em função de
de modo que todos os
trabalhos virtuais envolvidos no problema ficassem em função de
![]() , possibilitando assim, a solução da equação do princípio
dos trabalhos virtuais, uma vez que todos os trabalhos virtuais envolvidos no problema estavam em função de um único tipo de deslocamento.
, possibilitando assim, a solução da equação do princípio
dos trabalhos virtuais, uma vez que todos os trabalhos virtuais envolvidos no problema estavam em função de um único tipo de deslocamento.
Uma passagem crucial na tentativa de encontrar uma relação entre os vários
![]() 's que podem surgir na equação do PVT é a escolha do
sistema de coordenadas. A escolha adequada da origem do sistema pode facilitar sobremaneira a solução do problema, uma vez que uma escolha
equivocada pode dificultar muito ou até mesmo nos conduzir a resultados completamente errados. Um cuidado básico que se deve tomar quanto
a escolha da origem do sistema de coordenadas é a garantia de que o mesmo não se deslocará quando for imposto um deslocamento virtual ao
sistema de corpos rígidos. Para que as relações entre os
's que podem surgir na equação do PVT é a escolha do
sistema de coordenadas. A escolha adequada da origem do sistema pode facilitar sobremaneira a solução do problema, uma vez que uma escolha
equivocada pode dificultar muito ou até mesmo nos conduzir a resultados completamente errados. Um cuidado básico que se deve tomar quanto
a escolha da origem do sistema de coordenadas é a garantia de que o mesmo não se deslocará quando for imposto um deslocamento virtual ao
sistema de corpos rígidos. Para que as relações entre os
![]() 's seja correta é necessário que a origem do sistema de coordenadas seja
a mesma para tanto para o sistema indeslocado, quando para o sistema deslocado.
's seja correta é necessário que a origem do sistema de coordenadas seja
a mesma para tanto para o sistema indeslocado, quando para o sistema deslocado.