Equilíbrio de Mecanismos

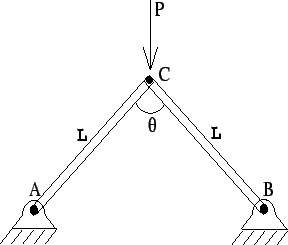
De modo bastante simplificado podemos dizer que os mecanismos são estruturas que não se sustentam por si próprias, e quando submetidos a forças se movimentam. O movimento se dá porque os vínculos não são suficientes para restringir o movimento. Do ponto de vista matemático, os mecanismos constituem sistemas onde o número de reações de apoio é menor que o número de equações de equilíbrio disponíveis para resolver o sistema de equações de equilíbrio.

Figure 9.2: Exemplo de estrutura hipoestática (mecanismo)

A Figura 9.2 apresenta um exemplo de mecanismo. São várias barras articuladas através de pinos que permitem o giro e que que estão igualmente apoiadas sobre dois pinos que também permitem o giro. A ``intuição mecânica'' <sup>9.1</sup> nos indica que essa estrutura ``irá cair'' devido as forças que atuam sobre a mesma, e que as reações de apoio nada podem fazer para impedir isso.

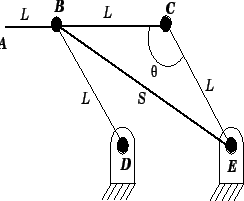
Digamos então que coloquemos um cabo ligando os pinos B e E, de modo a equilibrar o sistema, conforme mostrado na Figura 9.3

Figure 9.3: Equilibrando um mecanismo

Considerando que todas as barras tenham o mesmo comprimento, o problema consiste então em determinar qual o valor da tração no cabo BE em função da força $\vec{F}$ aplicada no ponto A. Esse é um dos exemplos clássicos de aplicação do método dos trabalhos virtuais na solução de probelmas envolvendo o equilíbrio de mecanismos.

Figure 9.4: Deslocamento virtual

A Figura 9.4 mostra um deslocamento virtual aplicado no mecanismo ABCDE, de modo a surgirem dois deslocamentos virtuais $\delta y$ e $\delta s$ nos pontos onde estão respectivamente aplicadas as forças $\vec{F}$ e a tração $\vec{T}$. Como somente estas forças estão aplicadas sobre pontos que se deslocam, somente elas provocarão o trabalho virtual. Como o deslocamento $\delta y$ tem o mesmo sentido da força $\vec{F}$ o trabalho de $\vec{F}$ será positivo, ao passo que o deslocamento $\delta s$ tem sentido contrário ao da tração $\vec{T}$, por isso o trabalho de $\vec{T}$ será negativo. Escrevendo a equação do trabalho virtual total, teremos que:

$$\bgroup\color{black} \sum W = W_F + W_T = (F \cdot \delta y) + (- T \cdot \delta s) = 0 \egroup$$

Portanto, podemos escrever que:

$$\bgroup\color{black} F \cdot \delta y = T \cdot \delta s \egroup$$

O problema agora consiste em achar uma relação entre $\delta y$ e $\delta s$, e isso pode ser feito a partir das seguintes observações da geometria do sistema.

Figure 9.5: Geometria do problema

Analisando a Figura 9.5, e fazendo BE=S podemos escrever que:

$$\bgroup\color{black} S^2 = L^2 + L^2 - 2L^2 cos \theta \egroup$$

Portanto,

$$\bgroup\color{black} 2S dS = - 2L^2 (-sen \theta) d \theta \egroup$$

$$\bgroup\color{black} dS = \frac{L^2 sen \theta}{S} d \theta \egroup$$

Do mesmo modo, podemos uma expressão para $\delta y$ em função de $\theta$:

$$\bgroup\color{black} y = L sen(180 - \theta) = L sen \theta \egroup$$

$$\bgroup\color{black} dy = L cos \theta d \theta \egroup$$

Voltando para a expressão original do trabalho virtual total pode-se escrever que:

$$\bgroup\color{black} F L cos \theta d \theta = \frac{T L^2 sen \theta}{S} d \theta \egroup$$

$$\bgroup\color{black} T = \frac{F S}{L} arctan \, \theta \egroup$$