Uma outra aplicação do método dos trabalhos virtuais consiste em calcular deslocamentos em estruturas isostáticas. Em nosso curso veremos os fundamentos dessa aplicação estudando deslocamentos infinitesismais em vigas isostáticas.
Para um considerável número 9.2 das vigas isostáticas usuais, o trabalho virtual das forças internas
pode ser expresso em função de um único esforço seccional que é o momento fletor, do seguinte modo:
Onde:
 É o momento de inérrcia da seção transversal em relação ao eixo neutro.
É o momento de inérrcia da seção transversal em relação ao eixo neutro.
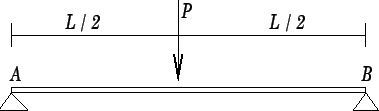
Vejamos um exemplo simples: Seja calcular o deslocamento no meio do vão de uma viga de comprimento
![]() devido a ação de
uma carga
devido a ação de
uma carga
![]() que também atua no meio do vão, conforme mostra a Figura 9.9:
que também atua no meio do vão, conforme mostra a Figura 9.9:
Em primeiro lugar, devemos calcular os valores das reações de apoio (verticais), que para o caso estudado serão iguais a
 ,
devido a simetria do problema. Uma vez que achamos os valores das reações de apoio podemos construir o gráfico do momento fletor
devido ao carregamento real
,
devido a simetria do problema. Uma vez que achamos os valores das reações de apoio podemos construir o gráfico do momento fletor
devido ao carregamento real
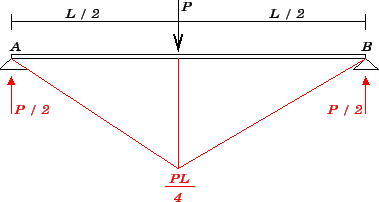
![]() . O gráfico do momento fletor devido a carga
. O gráfico do momento fletor devido a carga
![]() é apresentado na Figura 9.10.
é apresentado na Figura 9.10.
Agora que já temos as reações REAIS e o gráfico do MOMENTO FLETOR REAL, precisamos obter as reações virtuais e o gráfico
do momento fletor virtual. Para isso adotaremos a técnica da carga unitária virtual, que consiste em posicionar uma carga
virtual de intensidade unitária na posição exata onde desejamos calcular o deslocamento na estrutura isostática. No caso
do nosso problema, desejamos calcular o deslocamento no meio do vão da viga, portanto, iremos posicionar a carga virtual
unitária exatamente no meio do vão da viga.
Do mesmo modo que procedemos para a carga real devemos proceder para a carga virtual, ou seja, devemos calcular as reações de
apoio e obter o diagrama do momento fletor. Procedendo desse modo, teremos para o DMF da carga virtual, o diagrama apresentado
na Figura 9.11:
Agora que já temos os diagramas de
![]() e
e
 , devemos achar as expressões analíticas para essas duas curvas, para
que possamos integra-las conforme é indicado na Equação (9.4). Devido a simetria de geometria e carregamentos, podemos
nos contentar em achar uma expressão para curva do momento fletor válida apenas para meio vão e depois multiplicar os resultados
obtidos por dois, desse modo, podemos expressar
, devemos achar as expressões analíticas para essas duas curvas, para
que possamos integra-las conforme é indicado na Equação (9.4). Devido a simetria de geometria e carregamentos, podemos
nos contentar em achar uma expressão para curva do momento fletor válida apenas para meio vão e depois multiplicar os resultados
obtidos por dois, desse modo, podemos expressar
![]() e
e
 do seguinte modo:
do seguinte modo:
Substituindo os valores de (9.5) em (9.4), e lembrando que devemos multiplicar por dois os valores obtidos
pela integração, podemos expressar o trabalho virtual das forças internas do seguinte modo:
Resolvendo a Equação (9.6) chegaremos a seguinte expressão para o trabalho das forças internas:
E como a carga virtual que provocou o TRABALHO VIRTUAL EXTERNO foi igual a 1, temos a seguinte expressão para o trabalho virtual externo:
E como já sabemos que o trabalho virtual externo DEVE ser igual ao trabalho virtual interno, basta igualar as Equações (9.7) e
(9.8) para acharmos o valor do deslocamento no meio do vão, desse modo temos para a viga estudada que o deslocamento
![]() no
meio do vão devido a uma carga
no
meio do vão devido a uma carga
![]() posicionada igualmente no meio do vão será dado por:
posicionada igualmente no meio do vão será dado por:
Portanto, como vimos, o processo de cálculo do deslocamento segue etapas distintas, que consistem basicamente em calcular o valor do trabalho
virtual realizado pelas forças internas, uma vez que a técnica da carga unitária torna a expressão do trabalho externo bastante simples. Para
o cálculo de deslocamentos em vigas isostáticas, independente da geometria da viga e do carregamento, necessariamente teremos que passar pelas
seguintes etapas:
Felizmente para nós, para a grande maioria dos casos de
![]() e
e
 os valores de
os valores de
![]() encontram-se tabelados,
o que facilita muito a obtenção dos valores de deslocamentos em vigas isostáticas. Uma tabela que abrange um considerável número de combinações
entre
encontram-se tabelados,
o que facilita muito a obtenção dos valores de deslocamentos em vigas isostáticas. Uma tabela que abrange um considerável número de combinações
entre
![]() e
e
 pode ser encontrada em Süssekind [#!sussekind:1973!#]
pode ser encontrada em Süssekind [#!sussekind:1973!#]
[1] José Carlos Süssekind, Curso de Análise Estrutural. Editora Globo, São Paulo - SP,
![]() Edição, 1985.
Edição, 1985.