Representação analítica de vetores

Outra interessante abordagem ao se trabalhar com vetores está em se adotar a sua representação analítica, o que facilita o cálculo das operações vetoriais que veremos mais adiante. Obviamente, essa abordagem não inviabiliza a abordagem gráfica, porém se mostra bem mais eficiente quando estamos trabalhando no espaço vetorial tridimensional. Genericamente, podemos representar analiticamente um vetor do seguinte modo:

$$\vec{v} = x \vec{i} + y \vec{j} + z \vec{k}$$ (1.1)

Onde $x \vec{i}$, $y \vec{j}$ e $z \vec{k}$ são vetores que representam as projeções do vetor $\vec{v}$ sobre os eixos $x$, $y$ e $z$, repectivamente. Vamos entender melhor como isso funciona utilizando um exemplo bidimensional: Consideremos o vetor apresentado no exemplo 1, um vetor que tem origem em $(0,0)$ e extrmidade em $(3,4)$, conforme está mostrado na Figura 1.2.

Na realidade o que fizemos foi substiruir a representação do vetor $\vec{v}$ por uma soma vetorial cujo resultado é igual a $\vec{v}$. Entenderemos melhor isso mais adiante quando estiver-mos estudando a soma de vetores.

Figure 1.3: Projeções vetoriais em duas dimensões

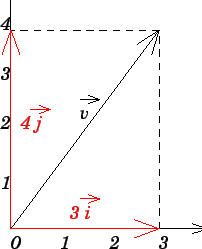
Como já calculamos anteriormente, esse vetor tem módulo igual a 5 e forma $53,13^{o}$ com o eixo $x$. Calculando o módulo da projeção desse vetor sobre o eixo $x$ acharemos o número 3, e prodecendo da mesma forma em relação ao eixo $y$ acharemos o número 4. Assim, podemos completamente descrever o vetor do exemplo 1 do seguinte modo:

$$\vec{v} = 3 \vec{i} + 4 \vec{j}$$ (1.2)

O caminho inverso também é perfeitamente possível, ou seja, dado um vetor $\vec{v} = 3 \vec{i} + 4 \vec{j}$ pode-se calcular o módulo e a direção desse vetor. Nesse caso, o módulo do vetor é calculado como sendo a raiz quadrada da soma dos quadrados dos módulos das projeções, ou seja:

$$\bgroup\color{black} \vert v\vert = \sqrt{3^2 + 4^2} \egroup$$

Os cossenos diretores são calculados da seguinte forma:

a)

$\lambda_x = \frac{proj_x}{\vert v\vert} = \frac{3}{5}$

b)

$\lambda_y = \frac{proj_y}{\vert v\vert} = \frac{4}{5}$

Onde $proj_x$ e $proj_y$ são respectivamente as projeções do vetor $\vec{v}$ sobre os eixos $x$ e $y$. Note que a soma dos quadrados dos cossenos diretores sempre é iagual a unidade.