Exemplo 1 - Cálculo de módulo e direção de vetor

Dado um vetor que tem origem em $(0,0)$ e extrmidade em $(3,4)$, determine o módulo e o ângulo que esse vetor forma com o eixo $x$.

Solução: Chamando o vetor de $\vec{v}$, calculamos o módulo e a direção de $\vec{v}$ do seguinte modo:

$$\bgroup\color{black} v = \sqrt{(3-0)^2+(4-0)^2} = 5 \egroup$$

$$\bgroup\color{black} \theta = cos^{-1}\left( \frac{3}{5} \right) = 53,13^{o} \egroup$$

Conforme vemos, o processo é bastante simples e pode ser utilizado em qualquer espaço vetorial, e como na totalidade dos casos estudados em nosso curso o maior espaço vetorial é o $\mathcal{R}^3$, adotaremos algumas abordagens que simplificarão nosso trabalho.

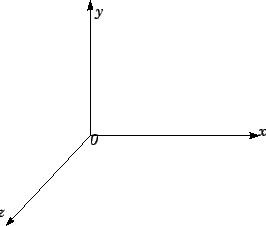
A primeira convenção que faremos se refere aos eixos coordenados: A figura 1.2 mostra o sentido positivos dos eixos. Portanto, todos as coordenadas de ponto, daqui por diante, terão como referencial o sistema de eixos apresentados na Figura 1.2:

Figure 1.2: Convenção de sinal para os eixos cartesianos de coordenadas

Outro procedimento bastante comum em Mecânica é se referir aos cossenos diretores de um vetor. Os cossenos diretores nada mais são do que a medida dos cossenos dos menores ângulos formados entre o vetor e as direções paralelas aos eixos coordenados. Como adotaremos a convenção de que os ângulos positivos são sempre medidos no sentido anti-horário, cossenos diretores negativos indicam ângulos no sentido horário.

Considerando o espaço vetorial tridimensonal teremos para cada vetor, três cossenos diretores, aos quais nominaremos de $\lambda_x$, $\lambda_y$ e $\lambda_z$, sendo respectivamente os cossenos dos ângulos formados entre o vetor e os eixos $x$, $y$ e $z$.