Teorema dos Eixos Paralelos

Consideremos o momento de inércia $I$ de uma superfície de área $A$ em relação a um eixo $AA'$, conforme o mostrado na Figura 7.3, de modo que $y$ é a distância de um elemento $dA$ ao eixo $AA'$. Desse modo podemos escrever que:

$$\bgroup\color{black} I_{AA'} = \int y^2 dA \egroup$$

Figure 7.3: Teorema dos eixos paralelos

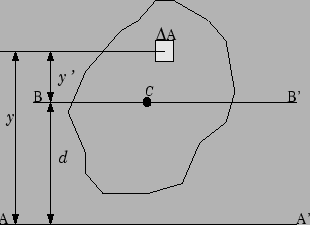
Consideremoas agora um eixo $BB'$ paralelo a $AA'$, passando pelo centróide $C$ da superfície. Se $y'$ é a distância de um elemento $dA$ ao eixo $BB'$ podemos escrever que $y = y'+ d$, conforme é mostrado na figura, sendo $d$ a distância entre os eixos paralelos $AA'$ e $BB'$

Se desejamos calcular o momento de inércia da superfície em relação ao eixo $AA'$ temos que:

$$I_{AA'} = \int y^2 dA = \int (y' + d)^2 dA = \int (y')^2 dA + 2d \int y'dA + d^2 \int dA$$ (7.3)

O termo $\int (y')^2 dA$ que aparece na Equação (7.3) corresponde ao momento de inércia da superfície em relação ao eixo que passa pelo centróide ( $BB'$), o qual denotaremos pelo símbolo $\overline{I}$. O termo $\int y'dA$ é o momento de primeira ordem da superfície em relação ao eixo que passa pelo centróide, e como já sabemos, É NULO. Finalmente, o termo $\int dA$ corresponde ao valor da área ( $A$), da superfície. Portanto, podemos reescrever a Equação (7.3) do seguinte modo:

$$\fbox{\rule[-.5cm]{0cm}{1.25cm} $ I = \overline{I} + Ad^2 $}$$ (7.4)

A Equação (7.4) é a forma mais conhecida do teorema dos eixos paralelos, que diz que o momento de Inércia de uma superfície $A$ em relação a um eixo qualquer $x$ é igual ao momento de inércia dessa mesma superfície $A$ em relação a um eixo $\overline{x}$ que passa pelo centróide e é paralelo a $x$ mais o produto entre a área da superfície e o quadrado da distância entre os eixos $x$ e $\overline{x}$.

O teorema dos eixos paralelos serve para obter o momento de inércia de uma seção em relação a um eixo, quando já sabemos o momento de inércia dessa mesma seção em relação a outro eixo, onde já se sabe o valor do momento de inércia, com a condição de que os dois eixos sejam paralelos. Vamos ver melhor como isso funciona ? Lembra da sugestão de exercício quando estávamos obtendo momento de inércia de uma superfície retangular por integração direta ? Vamos então calcular o momento de inécia de uma superfície retangular em relação a um eixo $\overline{x}$ que passa pelo centróide e é paralelo ao eixo $x$ que contém a base do retângulo. Usando a Equação (7.4) podemos escrever que:

$$\bgroup\color{black} \frac{bh^3}{3} = I_{\overline{x}} + (bh) \cdot \left( \frac{h}{2} \right)^2 \egroup$$

Portanto, se queremos obter $I_{\overline{x}}$, temos que:

$$\bgroup\color{black} I_{\overline{x}} = \frac{bh^3}{3} - \frac{bh^3}{4} = \frac{bh^3}{12} \egroup$$