Momentos de Inércia de Superfícies Compostas

Consideramos uma superfície composta A, aquela que pode ser dividida em várias superfícies componentes $\bgroup\color{black}$A_1$\egroup$ , $\bgroup\color{black}$A_2$\egroup$ , ..., $\bgroup\color{black}$A_i$\egroup$ , $\bgroup\color{black}$A_n$\egroup$ . Como a integral que representa o momento de inércia de A pode ser subdividida em integrais calculadas sobre $\bgroup\color{black}$A_1$\egroup$ , $\bgroup\color{black}$A_2$\egroup$ , ..., $\bgroup\color{black}$A_i$\egroup$ , $\bgroup\color{black}$A_n$\egroup$ , o momento de inércia de A em relação a um eixo dado, poderá ser calculado somando-se os momentos de inércia das superfícies $\bgroup\color{black}$A_1$\egroup$ , $\bgroup\color{black}$A_2$\egroup$ , ..., $\bgroup\color{black}$A_i$\egroup$ , $\bgroup\color{black}$A_n$\egroup$ em relação ao mesmo eixo. Lembrando de que as $\bgroup\color{black}$n$\egroup$ parcelas de cada superfície na composição do momento de inércia da área total deve ser obtida ustilzando o teorema dos eixos paralelos. Vejamos um exemplo simples:

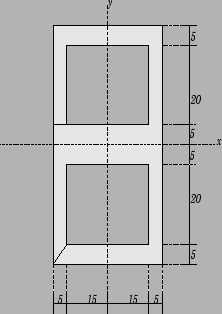
Seja calcular o momento de inércia da superfície apresentada na Figura 7.4 em relação aos eixos $\bgroup\color{black}$x$\egroup$ e $\bgroup\color{black}$y$\egroup$ apresentados na mesma figura.

**Figure 7.4:** Aula 7 - Exemplo 2
$\resizebox{50mm}{70mm}{ % \vspace{-20mm} % \includegraphics{/home/marvinsc/Academico/Ueg/Mecanica/2001_1/Aulas/Figuras/aula7_exemplo2.eps}}$

Como na maioria dos problemas de mecânica existe mais de uma forma de chegar a solução, apresentaremos agora uma tabela que facilita a organização dos cálculos.

Figura	eixo	$\bgroup\color{black}$\overline{I}$\egroup$	Área	d	I

	x	$\bgroup\color{black}$7,2 \cdot 10^5$\egroup$	2400	30	$\bgroup\color{black}$2,88 \cdot 10^6$\egroup$
1
	y	$\bgroup\color{black}$3,2 \cdot 10^5$\egroup$	2400	20	$\bgroup\color{black}$1,28 \cdot 10^6$\egroup$


	x	$\bgroup\color{black}$2,0 \cdot 10^4$\egroup$	600	45	$\bgroup\color{black}$1,235\cdot 10^6$\egroup$
2
	y	$\bgroup\color{black}$4,5 \cdot 10^4$\egroup$	600	20	$\bgroup\color{black}$2,85 \cdot 10^5$\egroup$


	x	$\bgroup\color{black}$2,0 \cdot 10^4$\egroup$	600	5	$\bgroup\color{black}$3,50 \cdot 10^4$\egroup$
3
	y	$\bgroup\color{black}$4,5 \cdot 10^4$\egroup$	600	20	$\bgroup\color{black}$2,85 \cdot 10^5$\egroup$

$\begin{displaymath}\bgroup\color{black} \sum I_x = 2,88 \cdot 10^6 - 1,235 \cdot 10^6 - 3,50 \cdot 10^4 = 1,61 \cdot 10^6 \; uc^4\egroup\end{displaymath}$

$\begin{displaymath}\bgroup\color{black} \sum I_y = 1,28 \cdot 10^6 - 2,85 \cdot 10^5 - 2,85 \cdot 10^5 = 7,10 \cdot 10^5 \; uc^4\egroup\end{displaymath}$

Onde $\bgroup\color{black}$uc$\egroup$ = unidade de comprimento. A figura 1 é o retângulo que envolve toda a superfície, considerado cheio, as figuras 2 e 3 são os retângulos contidos no interior da figura, considerados como sendo vazios. Na soma das inércias, aquelas oriundas de áreas consideradas vazias entram com sinal negativo.