Momentos de Inércia de Superfícies por Integração

O procedimento para calcular os momentos de segunda ordem por integração direta é idêntico ao utilizado para calcular os momentos de primeira ordem. Dentre as inúmeras formas possíveis pode-se adotar a sugerida na aula 06 quando estávamos calculando os momentos de primeira ordem por integração direta. Relembrando, temos:

1. Escolhe-se uma faixa de largura $dx$, paralela ao eixo $y$ ou uma faixa de largura $dy$, paralela ao eixo $x$.
2. Escreve-se a expressão que define a área $dA$, da faixa escolhida
3. Calculam-se os momentos de segunda ordem $I_x=\int y^2 dA$ e $I_y=\int x^2 dA$.

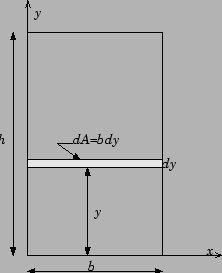
Vejamos um exemplo: Seja calcular os momentos de segunda ordem de uma superfície retangular de base $b$ e altura $h$ em relação aos eixos $x$ e $y$ que passam respectivamente pela base da seção e pelo bordo mais a esquerda.

Figure 7.2: Aula 7 - Exemplo 1

Para esse exemplo escolheremos uma faixa paralela ao eixo $x$ e de largura igual a $dy$. Para este caso temos que: $dA = b dy$, portanto:

$$\bgroup\color{black} I_x = \int y^2 dA = \int y^2 b dy = b \int_{0}^{h} y^2 dy = \frac{bh^3}{3} \egroup$$

Note que devido a faixa ser paralela a $x$, os limites de integração foram de $0$ a $h$. De modo análogo podemos obter $I_y$, só que agora tomando uma faixa paralela a $y$ e de largura $dx$, Para esse caso temos que: $dA = h dx$, e portanto:

$$\bgroup\color{black} I_y = \int x^2 dA = \int x^2 h dx = h \int_{0}^{b} x^2 dx = \frac{hb^3}{3} \egroup$$

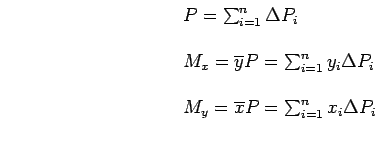Sugestão: Calcule os momentos de segunda ordem para a mesma seção retangular, considerando agora os eixos $\overline{x}$ e $\overline{y}$, respectivamente paralelos a $x$ e $y$ e passando pelo centróide da seção.