Até agora vimos o que é baricentro e o que é centróide de uma superfície plana, e aprendemos duas formas distintas para calcular as coordenadas desses pontos notáveis de uma superfície. Para facilitar nossa semântica, daqui por diante consideraremos todas as superfícies homogêneas e de espessura constante, e sob essas condições passaremos a utilizar apenas o termo centróide, uma vez que o mesmo coincidirá com o baricentro da superfície.
Os exemplos apresentados para o cálculo das coodenadas do centróide foram bastante simples, mas ilustram o procedimento geral para o cálculo
das coordenadas, seja utilizando a decomposição de figuras planas, seja utilizando a integração direta das equações (6.7). Resta agora
exercitar esse procedimento através da solução de outros exercícios.
As aplicações para os procedimentos que apredemos até aqui (nessa aula) são diversas, porém, as que serão mais utilizadas por nós são aquelas
que dizem respeito ao posicionamento da força peso e ao cálculo de áreas superficiais e volumes de sólidos. O cálculo de áreas superficiais e
volumes de sólidos em função de centróides será mais adiante detalhado através do teorema de Pappus e Guldin, e um exemplo de posicionamento
da força peso, já pode ser apresentado agora:
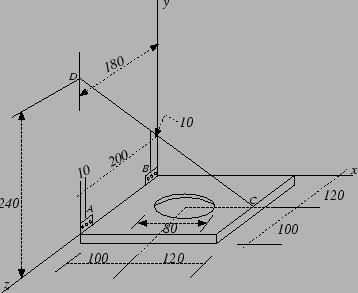
Seja calcular a tensão no cabo (CD) de sustentação da prateleira apresentada na Figura 6.8, sabendo que os apoios A e B são dobradiças
que não exercem empuxo axial e que a prateleira tem espessura de 10 mm e é constituída de um material cuja massa específica é de
![]() .
Considere
.
Considere
 .
.