Teorema de Pappus e Guldin

O teorema de Pappus e Guldin para para o cálculo de áreas de superfícies de revolução diz o seguinte: A área de uma superfície de revolução é igual ao produto entre o comprimento de sua linha geratriz pelo comprimento da distância percorrida pelo centróide da geratriz durante a revolução da mesma.

Figure 6.9: Superfície de revolução

Vejamos um exemplo para o caso do cáclulo da área superficial de uma superfície gerada a partir da revolução de uma linha de comprimento $L$ ao redor do eixo $x$, sendo $L$ paralela a $x$ e distante $Yc$ deste. Como o centróide da linha, neste caso particular, está contido sobre a mesma, temos, pelo teorema de Pappus e Guldin:

$$\bgroup\color{black} A_s = 2 \times \pi \times Yc \times L\egroup$$

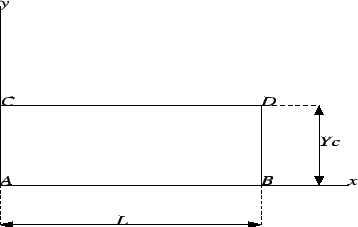
O teorema de Pappus e Guldin para o cálculo de volumes de revolução diz o seguinte: O volume de um sólido de revolução é igual ao produto da área da superfície geratriz pela distância percorrida pelo centróide da superfície geratriz durante a revolução.

Figure 6.10: Sólido de revolução

Vejamos um exemplo para o caso do cálculo do volume de um sólido gerado pela revolução da superfície ABCD, apresentada na Figura 6.10, em torno do eixo $x$. Como o centróide da superfície está $Yc / 2$ distante do eixo $x$, temos que o volume do sólido de revolução será dado por:

$$\bgroup\color{black} V_s = 2 \times \pi \times \frac{Yc}{2} \times L \times Yc \egroup$$