Bom, agora que já relembramos um pouco mais de álgebra vetorial, vamos definir em termos matemáticos o que o momento de uma força em relação a um
eixo. Uma definição possível é a seguinte: O momento de uma força
![]() em relação a um eixo
em relação a um eixo
 é igual a projeção sobre esse mesmo eixo
é igual a projeção sobre esse mesmo eixo
 ,
do momento de
,
do momento de
![]() em relação a um ponto qualquer contido no eixo
em relação a um ponto qualquer contido no eixo
 .
.
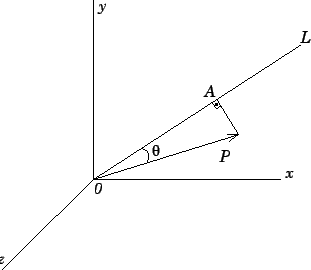
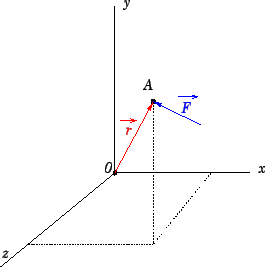
Complicou ? não deu para entender de primeira ? então vamos com calma. Para entender melhor a definição acima, vamos analisar a Figura 4.3:
Vamos definir novamente, agora olhando para a Figura 4.3: O momento de
![]() em relação ao eixo
em relação ao eixo
 é igual a
projeção de
é igual a
projeção de
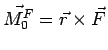 sobre o eixo
sobre o eixo
 . Ora, já sabemos que
. Ora, já sabemos que
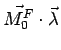 , e também sabemos
que a projeção de
, e também sabemos
que a projeção de
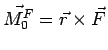 sobre o eixo
sobre o eixo
 pode ser dada por
pode ser dada por
![]() , onde
, onde
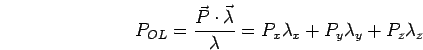 é um vetor unitário no mesmo sentido e direção do eixo
é um vetor unitário no mesmo sentido e direção do eixo
 . Portanto, agora só nos resta escrever que:
. Portanto, agora só nos resta escrever que:
Onde
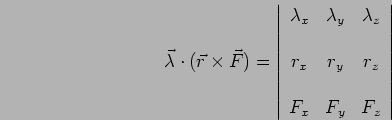 é o momento da força
é o momento da força
![]() em relação ao eixo
em relação ao eixo
 . Como podemos perceber, o momento de uma força em
relação a um eixo é matematicamente expresso em termos de um produto misto de três vetores, que pode ser expresso em termos
de um determinante do seguinte modo:
. Como podemos perceber, o momento de uma força em
relação a um eixo é matematicamente expresso em termos de um produto misto de três vetores, que pode ser expresso em termos
de um determinante do seguinte modo:
| (4.19) |
Agora que já sabemos obter o momento de uma força em relação a um eixo, vamos fazer dois exercícios interessantes: Primeiro: Determine
o momento de uma força em relação aos eixos coordenados, ou seja, determine
![]() ,
,
![]() e
e
![]() . Segundo: Dado
um sistema cartesiano com origem em
. Segundo: Dado
um sistema cartesiano com origem em
 obtenha o momento de uma força
obtenha o momento de uma força
![]() , aplicada em um ponto
, aplicada em um ponto
![]() , em relação a um eixo qualquer
que passe por um ponto
, em relação a um eixo qualquer
que passe por um ponto
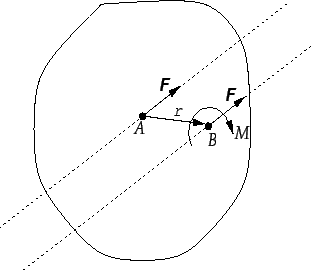 , ambos no espaço e de coordenadas não nulas. Entendeu ? se entendeu, mãos a obra !
, ambos no espaço e de coordenadas não nulas. Entendeu ? se entendeu, mãos a obra !
Também já está na hora de exercitar os conhecimentos adquiridos, que tal fazer todos os exercícios pares do capítulo três do Beer e Jhonston ?
(é uma boa sugestão)