Graficamente, somar vetores consiste em colocar a origem de um na extremidade de outro e assim consecutivamente, até
posicionar-mos o último vetor da soma. Portanto, se estamos somando
![]() basta transportar a origem do
vetor
basta transportar a origem do
vetor
![]() para a extremidade do vetor
para a extremidade do vetor
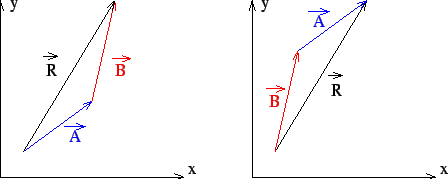
![]() conforme o ilustrado na Figura 1.4. Na mesma figura
podemos perceber que a soma vetorial goza da propriedade comutativa, ou seja, o resultado de
conforme o ilustrado na Figura 1.4. Na mesma figura
podemos perceber que a soma vetorial goza da propriedade comutativa, ou seja, o resultado de
![]() é o mesmo
que o de
é o mesmo
que o de
Do ponto de vista analítico, somar dois vetores consiste apenas em somar as projeções cartesianas correnspondentes,
assim, ao somar os vetores
![]() e
e
![]() obteremos o vetor
obteremos o vetor
![]() , portanto
, portanto
![]()
O que foi visto para duas dimensões aplica-se igualmente para três dimensões, onde já é possivel perceber a grande
vantagem de trabalhar com a representação analítica dosvetores. Porém é sempre bom para o estudante de mecânica
fazer o exercíio de ``visualizar'' o problema.
Na soma vetorial, o sinal negativo apenas quer dizer que o vetor está orientado no sentido contrário ao convencionado
como positivo para os eixos coordenados (Figura 1.2).