Produto de um escalar por um vetor

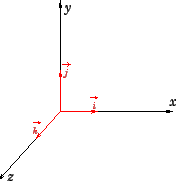
Antes de discutirmos propriamente o produto de um escalar por um vetor, vamos introduzir o conceito de vetor unitário: Vetor unitário nada mais é do que um vetor de módulo igual a 1. Se esse vetor unitário está sobre o eixo $x$, ele será batizado de $\vec{i}$, da mesma forma teremos os vetores $\vec{j}$ e $\vec{k}$, vetores unitários sobre os eixos $y$ e $z$, respectivamente.

Lembra da representação cartesiana de um vetor ? Pois bem, lá já apareceram os vetores unitários, e também o produto de um vetor por um escalar. Na realidade o produto de um vetor por um escalar nada mais é do que uma soma consecutiva de um mesmo vetor. Ou seja, ao invés de se escrever $\vec{B}=\vec{A}+\vec{A}+\vec{A}+\vec{A}+...+\vec{A}$ $N$ vezes, opta-se por escrever $\vec{B}=N \cdot \vec{A}$.

Como as projeções dos vetores sobre os eixos coordenados serão sempre um múltiplo da unidade, utilizamos os vetores unitários para decompor um vetor qualquer em uma soma de vetores múltiplos dos vetores unitários.

Figure 1.5: Vetores unitários

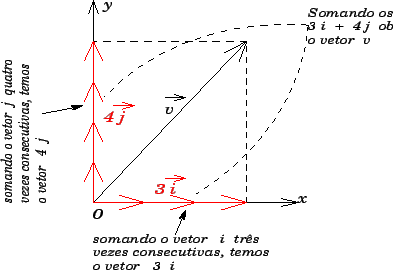
Vamos mais uma vez recorrer ao vetor apresentado no exemplo um para ilustrar as idéias de vetor unitário, de produto de um escalar por um vetor e de soma vetorial. No exemplo um tínhamos um vetor $\vec{v} = 3 \vec{i} + 4 \vec{j}$. Ou seja, o vetor $\vec{v}$ é igual a soma dos vetores $3\vec{i}$ e $4\vec{j}$. Por outro lado o vetor $3\vec{i}$ nada mais é do que a soma dos vetores $\vec{i}+\vec{i}+\vec{i}$ e do mesmo modo o vetor $4\vec{j}$ é a soma consecutiva de quatro vetores $\vec{j}$.

Figure 1.6: Soma vetorial

Ainda teremos que ver outras operações vetoriais tais como produto escalar, produto vetorial e produto vetorial misto, porém, para o momento as noções de soma vetorial e de produto de um escalar por um vetor já nos bastam para começarmos a falar de força.