Electrical Fundamentals.
The Bipolar Junction Transistor.

Here is another small excerpt from my textbook. See Semiconductor Diodes for details.
Chapter 4.
Transistors as Switches and Amplifiers.
The development of the transistor was the greatest single advancement in electronics since the development of the vacuum tube in the early part of the 20th century. Some people might ask "What about the integrated circuit?" The integrated circuit is just a more compact way of packaging circuitry. In fact, there was a little known attempt in the early 1960s to put vacuum tubes in an integrated package. The information available to the writer indicates that a prototype was actually constructed and tested. The demise of the vacuum tube has relegated this experiment to the dusty back shelves of history. But we digress -- oh yes -- the transistor. Even the very earliest of transistors occupied about 1/100 the volume of the average vacuum tube. Such a large change was bound to start a revolution and it did.
4.1 The Bipolar Junction Transistor (BJT).
The full name of the tiny transistor is quite a mouthful. That is, no doubt, why it is rarely called by that name. Even people who don't know what a transistor looks like know the shortened name "transistor". Non-technical people are unaware that there are two major types of transistors, bipolar junction transistors and field effect transistors. The term "transistor" is too imprecise for our purposes. Instead of using the full name every time, we will use the acronym BJT.
A BJT will allow a small current in one circuit loop to control a much larger current (typically 100 times larger) in another circuit loop. The nature of the BJT is such that the current in the second loop may be switched (turned on and off) or varied by an arbitrarily small amount. We will be devoting much space in following sections to the circuits which permit the BJT to be used to control large currents. In this section we will study the internal physics of the BJT and try to understand how it does what it does.
A simplified cross-section of a BJT is shown in Figure 4.1. A bipolar junction transistor consists of three layers of alternating semiconductor type. These three layers have been given the names emitter, base and collector.

Figure 4.1 Simplified Drawing of a BJT With Supply Voltages
For a verbal description click here.
BJTs may be manufactured in either of two forms. In one form the emitter is P type semiconductor, the base is N type semiconductor and the collector is P type semiconductor. Such transistors are referred to as PNP transistors. In the other form the emitter is N type semiconductor, the base is P type semiconductor and the collector is N type semiconductor. Such transistors are referred to as NPN transistors. (The designation NPN or PNP informs the reader that the transistor is a bipolar junction type and the term NPN transistor is precise.) In the example of Figure 4.1 the transistor is an NPN type which means that the emitter is N type semiconductor, the base is P type semiconductor and the collector is N type semiconductor.
The connection of the battery on the left is such as to forward bias the P-N junction between the emitter and base. The voltage drop across the emitter-base junction is about 0.6 volts. (We used 0.7 volts in rectifier circuits because the current is fairly high. In the base circuit of a BJT the currents are fairly small, typically a few tens of microamperes and the voltage drop is more typically 0.6 volts.) The collector supply voltage, V_CC may be anywhere between 5 volts and the maximum the transistor will stand. With the base at +0.6 volts and the collector at more than +5 volts, the base-collector junction is reverse biased.
The forward biased emitter-base junction causes majority carriers to move across the junction. These charge carriers become minority carriers as soon as they cross the junction. Minority carriers do not immediately combine with majority carriers but will travel a short distance until statistics catch up with them and recombination occurs. The average distance a minority carrier can cover is called the mean free path. In a real transistor the width of the base region is less than the mean free path of a minority carrier in the base. That means that most of the minority carriers which are injected into the base region will make it across the base without being recombined with majority carriers from the base. As soon as a minority carrier exits the base and enters the collector, it is again a majority carrier. Majority carriers which are injected into the collector will constitute a collector current. That collector current originated in the emitter and is controlled by the base current.
In the specific case of the NPN transistor shown in Figure 4.1 the base supply voltage VBB will cause a base current to flow into the base. That will cause holes from the base to cross into the emitter and electrons from the emitter to cross into the base. The holes from the base will simply recombine with electrons in the emitter. Some electrons from the emitter will flow out through the base connection and back to VBB but most of the electrons which cross the emitter-base junction will continue on to cross the base-collector junction. Thus there are electrons originating in the emitter region and ending up in the collector region.
If the base current is increased, the number of charge carriers injected into the base will be increased and so will the number of carriers injected into the collector. More base current means more collector current. Less base current means less collector current. The animation below shows this. If the base current is shut off, the collector current will cease to flow. The collector current is typically 100 times larger than the base current.

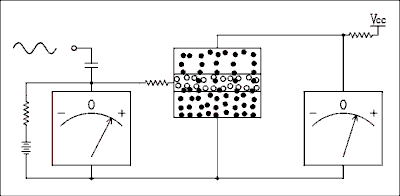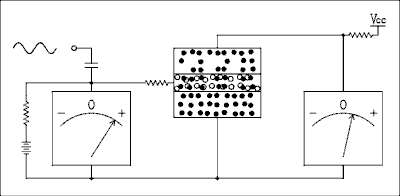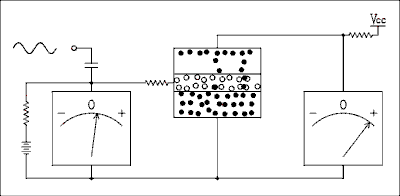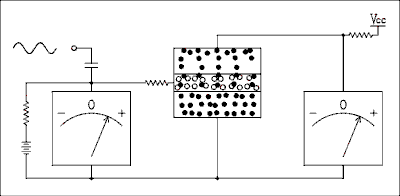
Figure 4.1a Animation showing holes and electrons in a BJT.
For a verbal description click here.
If a PNP transistor were to be used in the circuit of Figure 4.1, it would be necessary to reverse both batteries. The discussion above will apply to a PNP transistor, the only changes to be made are to change every occurrence of "electron" to "hole" and "hole" to "electron". All references to majority and minority carriers remain as they are.
Figure 4.2 is a repeat of Figure 4.1 but with the schematic symbol for an NPN transistor instead of the representation of the transistor's innards. We will now define a transistor parameter. It is called the forward DC current gain. It is assigned the symbol beta and is
beta = I_C / I_B (4.1)
where I_C is the DC collector current and I_B is the DC base current of the transistor. Equation 4.1 is a definition and so cannot be derived.

Figure 4.2 Schematic of a Properly Biased NPN Transistor.
For a verbal description click here.
By applying Kirchhoff's and Ohm's laws to the circuit of Figure 4.2 it is possible to write some other equations. Summing currents we have
I_E = I_C + I_B (4.2)
where I_E is the emitter current. Summing voltages around the base loop we have
V_BB = I_B R_B + V_BE (4.3)
where V_BE is the base to emitter voltage drop, which is approximately 0.6 volts. If we substitute V_BE = 0.6 v and rearrange equation 4.3 we have
I_B = (V_BB - 0.6 v) / R_B (4.4)
In the collector loop we can write
V_CC = I_C R_C + V_CE (4.5)
where V_CE is the voltage between collector and emitter. In a great many circuits V_CE is taken as the output voltage of the transistor circuit. Rearranging equation 4.5 we have
V_CE = V_CC - I_C R_C (4.6)
If we combine equations 4.1, 4.4 and 4.6 we have
V_CE = V_CC - beta R_C (V_BB - 0.6 v) / R_B (4.7)
V_CE can never, repeat NEVER, change sign. The absolute value of V_CC must always be greater than the absolute value of V_CE in equation 4.7. V_CE can never exceed V_CC because to do so would require that the term on the right in equation 4.7 undergo a change of sign. That cannot happen in the real world. Because the base-emitter junction is a P-N junction diode, if VBB becomes less than 0.6 volts, the base current will simply stop, not reverse. V_CE will be equal to V_CC.
Within the limits 0 to V_CC notice that if V_BB is decreased, V_CE is increased and visa versa. These are common emitter equations and may not apply to all circuits employing bipolar transistors.
The important thing about these seven equations is to understand how they were obtained. If you do not understand how these equations were obtained it is guaranteed that the rest of this chapter will be Greek to you.
Go back home.
4.2 The BJT as a Switch.
As mentioned above if the base current is removed from a transistor, the collector current will become similar to the reverse current in a diode, (too small to measure). Thus if a small current is turned on and off in the base of a BJT, the collector current will be turned on and off. Because the collector current is much larger than the base current, a low power circuit can be made to turn a high power device on and off. An excellent example of this is an indicator light.

Figure 4.3 BJT Switch Turns Light On and Off
For a verbal description click here.
Figure 4.3 shows how a transistor can be used to turn a light on and off. It is very common in both consumer and laboratory equipment for a light to come on to indicate that a particular function has been activated. The input terminals on the left connect to what will be referred to as the driving source. The driving source is not capable of delivering enough current to light the lamp. This low power circuit will deliver a voltage when the light is to be on and no (or very little) voltage when the light is to be off.
An ideal switch has infinite resistance when it is open and zero resistance when it is closed. The BJT is quite close to being ideal in the open (off) condition but in the closed (on) condition it is not quite perfect. The on condition is known as saturation and is the condition wherein the collector current is as large as it can be. When a transistor is in saturation V_CE is about 0.1 or 0.2 volts.
When a BJT is in saturation, most of the power supply voltage will appear across the load (device being switched on and off) and so the current through the load is
I_SAT = (V_CC - V_{CE_SAT}) / R_L (4.8)
where V_CC is the power supply voltage, R_L is the load resistance and 0.1 v < V_{CE_SAT} < 0.2 volts.
Example 4.1.

A lamp having a resistance of 22 ohms is to be switched by a BJT. The power supply voltage is 5 volts and the collector saturation voltage is 0.1 volts. What is the saturation current of the transistor? See Figure 4.3.

Solution:

I_SAT = (5 v - 0.1 v) / 22 ohms = 223 mA

Trouble can develop in switching circuits if the transistor is not in saturation. To place a transistor in saturation it is necessary to supply more base current than is needed to just barely place the transistor in saturation. To be absolutely certain that the transistor is in saturation, the base current should be at least twice that required to just barely saturate the transistor. It will not do any damage if the base current is larger than that required for saturation. The collector current cannot be any greater than the saturation current.
Example 4.2.

Using the same conditions from example 4.1, what is the minimum base current required to place the transistor in saturation if beta is 80?

Solution:

I_{B_MIN} = I_SAT / beta = 223 mA / 80 = 2.79 mA
The resistor in the base circuit must be properly selected so as to cause the base current to be large enough to place the transistor in saturation. On the other extreme the driving source will have a practical limit to how much current it will supply. If there were no limit, the load could be connected to the source and the switching transistor would not be needed.
Example 4.3.

Continuing with examples 4.1 and 4.2, what is the range of resistance for R_B if the driving source can supply a maximum of 12 mA at a voltage of 5 volts. What should the resistance be to give a saturation safety factor of 2.5?

Solution:

In example 4.2 the minimum base current was calculated to be 2.79 mA. The maximum base current is the maximum which the driving source can supply, which is given as 12 mA. Solving equation 4.4 for R_B we have
R_B = (V_BB - 0.6 v) / I_B
R_{B_MIN} = (5 v - 0.6 v) / 12 mA = 367 ohms.
R_{B_MAX} = (5 v - 0.6 v) / 2.79 mA = 1.58 k ohms.
Since the minimum base current for saturation is 2.79 mA
a safety factor of 2.5 calls for a base current of 6.98
mA. R_B = (5 v - 0.6 v) / 6.98 mA = 630 ohms.
A 620 ohms standard value resistor would be used.
Another consideration in switching transistor circuits is whether the transistor will be turned off when it is supposed to be off. As long as the voltage of the driving source goes below about 0.6 volts, the transistor will most likely be turned off. But some driving sources do not go below 0.6 volts and the transistor may not be completely turned off.
Example 4.4.

In Figure 4.3 it is now assumed that V_CC is 5 volts, the resistance of the lamp is 22 ohms, the resistance of R_B is 620 ohms and the beta of the transistor is 80. The driving source has an "on" voltage of 5 volts. (a) If its "off" voltage is 0.2 volts, is the transistor off? If not, what is the collector current? (b) If the driving source has an "off" voltage of 1.0 volts, is the transistor off? If not, what is the collector current?

Solution:

(a) The driving source has an "off" voltage of 0.2 volts. That is less than the 0.6 volt breakdown of the base-emitter junction. There will be no base current and so there will be no collector current. The transistor switch will be off.
(b) If the "off" voltage of the driving source is 1 volt there will be some base current. The base current will be I_B = (1 v - 0.6 v) / 620 ohms = 0.645 mA; the collector current will be 80 x 0.645 mA = 51.6 mA. Although they are not asked for in the original example we will calculate the drop across the load and V_CE to give a complete illustration of this type of problem. The drop across the load is I_C R_L = 51.6 mA x 22 ohms = 1.14 volts. V_CE is V_CC - V_L = 5 v - 1.14 v = 3.86 volts.
As you can see in the above example the transistor is "mostly" off. The lamp would glow slightly. An operator might be confused and become unsure as to whether a particular function is engaged or not. In something such as a nuclear power plant such confusion could be the difference between safe and unsafe operation. It is highly undesirable for indicator lamps to be partially on when they are supposed to be off.
Figure 4.4 shows a circuit which will overcome the problem of a driving source which will not go to zero for the off state.

Figure 4.4 Switching Circuit for Non-zero Driving Sources
For a verbal description click here.
The procedure for solving this circuit is as follows.

Assume that there is no load on the voltage divider in the base circuit and see if the transistor will be turned on or not. If the calculated voltage exceeds 0.6 volts, the transistor is at least part way on. If the voltage is less than 0.6 volts the transistor is off.

To calculate the base current in the "on" state assume that V_BE is 0.6 volts and calculate the current through R₂ (the voltage across R₂ will be 0.6 volts).

Calculate the current through R₁ assuming V_BE to be 0.6 volts.

The current through R₁ will split. Some will go through R₂ and the rest will go into the base of the transistor. To obtain the base current subtract the R₂ current from the R₁ current.

For those who would rather memorize an equation it is
I_B = (V_{DS_ON} - 0.6 v) / R₁ - 0.6 v / R₂ (4.9)
where V_{DS_ON} is the on voltage of the driving source. It should be pointed out and emphasized that V_BE for a good (not burned out) BJT can never exceed about 0.6 or 0.7 volts. If it does in a calculation, something has been neglected but no damage is done. If V_BE exceeds 0.7 volts in the real world, the BJT is burned out. If it wasn't before, it is now.
Example 4.5

For the values given in Figure 4.4 will a driving source which has an on voltage of 5 volts and an off voltage of 1 volt turn the BJT switch on and off?

Solution:

For the off state V_BE = 1 v x 1 k ohms / (5.6 k ohms + 1 k ohms) = 0.15 v; the BJT switch is off. For the on state V_BE = 5 v x 1 k ohms / (5.6 k ohms + 1 k ohms) = 0.76 v; there will be base current. Calculating the amount of base current
I_B = V_{DS_ON} - 0.6 v) / R₁ - 0.6 v / R₂ = 4.4 v / 5.6 k ohms - 0.6 v / 1 k ohm = 0.186 mA
The base current required to turn the switch on is I_B = I_C / beta and I_C = R_C / V_CC = 12 v / 150 ohms = 80 mA, I_B = 80 mA / 100 = 0.8 mA. With 0.8 mA required and 0.186 mA supplied, there is insufficient base current to turn the BJT switch on.

Example 4.6

Will a driving source of 10 volts turn the BJT on in Figure 4.4?

Solution:

We know from example 4.5 that 5 volts is enough to slightly forward bias the base-emitter junction and so we do not need to test to see if 10 volts will do it. Calculating I_B gives
I_B = (10 v - 0.6 v) / 5.6 k ohms - 0.6 v / 1 k ohm = 1.08 mA.
In example 4.5 we saw that 0.8 mA was required to turn the BJT on and we have 1.08 mA. The BJT is on.
BJT switches are used whenever a device such as a microprocessor needs to switch the current to any device which draws more current than the microprocessor can supply. Devices which may be switched include lamps, relays, buzzers and digital displays.
Go back home.
4.3 The BJT as an Amplifier.
An amplifier is any sort of device which will increase the magnitude of a signal. An amplifier may increase the magnitude of the voltage, current or both but to qualify as a true amplifier it must increase the power of a signal. A transformer can be used to increase the voltage of a signal, but there is no increase in power and a transformer is not an amplifier.
To characterize an amplifier completely it is necessary to know four things about it. They are

the relationship between the input voltage and the input current,

the relationship between the output voltage and the output current,

a relationship showing how the output is affected by the input, and

a relationship showing how the input is affected by the output.

These characteristics are called the four-terminal network parameters.
There are three groups of parameters, the impedance parameters, the admittance parameters and the hybrid parameters. All four of the impedance parameters have units of ohms and all four of the admittance parameters have units of ohms^-1. The hybrid parameters are a mix of units.

Figure 4.5 Generalized Four-terminal Network
For a verbal description click here.
Figure 4.5 shows a generalized four-terminal network. The open circuit impedance parameters are as follows.

Input Impedance Z₁₁ = V₁ / I₁ with I₂ = 0

Output Impedance Z₂₂ = V₂ / I₂ with I₁ = 0

Forward Transfer Impedance Z₁₂ = V₂ / I₁ I₂ = 0

Reverse Transfer Impedance Z₂₁ = V₁ / I₂ I₁ = 0
"What has all of this to do with transistors?" A transistor can be treated as a four-terminal network. "Hold on now, you said a transistor has three terminals, emitter, base and collector, I remember that!" Correct. We will use one of the terminals twice so as to use four-terminal network parameters on a BJT.
Let us apply the hybrid parameters to the common emitter configuration. That means that the input is applied between the base and emitter and the output is taken between the collector and emitter as indicated in Figure 4.6a.
In the equations to follow all of the voltages and currents are AC small signal. Small signal means that the AC voltages are small enough so that the natural nonlinearities of P-N junctions are not significant and the I-V characteristics "look" linear. This is not an unrealistic condition. All amplifier transistors must be used in this way to avoid signal distortion. Distortion is any unwanted alteration of the signal.
The small-signal common-emitter hybrid parameters for the BJT are as follows.
The short-circuit input impedance.
h_ie = v_be / i_b with v_ce = 0 (4.10)
The open-circuit output admittance.
h_oe = i_c / v_ce with i_b = 0 (4.11)
The short-circuit forward current transfer ratio.
h_fe = i_c / i_b with v_ce = 0 (4.12)
The open-circuit reverse voltage transfer ratio.
h_re = v_be / v_ce with i_b = 0 <(4.13)
Just in case you are wondering, h_re is measured by injecting a signal at the collector and making a measurement at the base. These parameters are all definitions.

Figure 4.6 (a) BJT and (b) Four-terminal Equivalent Circuit.
For a verbal description click here.
The hybrid parameters give rise to the equivalent circuit of Figure 4.6b. This circuit takes the place of the transistor and is considered to be equivalent to it. The parameter h_ie is the input resistance. It is connected in series with the voltage generator which represents h_re. The presence of h_re indicates that a small amount of the output voltage is fed back into the base-emitter loop. In the collector-emitter loop a resistor representing h_oe and a current source representing h_fe are connected in parallel. Although h_oe is expressed as a conductance, it is the reciprocal of the output resistance of the transistor. The current produced by the current source h_fe is equal to h_fe times the current in the base loop.
A generator may be connected, (in thought), to the base- emitter side of the equivalent circuit and a load resistance connected to the collector-emitter side. Equations may then be derived for such things as the input impedance, the output impedance and the gain. These equations are indeed complex. Advancing technology has saved us from having to deal with these equations.
The voltage feedback which is represented by h_re is caused by the electric field within the transistor which is produced by the collector-to-emitter voltage. This field affects the concentration of charge carriers within the base and causes the forward voltage drop across the base-emitter junction (V_BE) to be affected by the magnitude of V_CE. The same electric field causes the collector current to increase as V_CE increases. The value of h_oe is the slope of the graph of IC versus V_CE. Modern transistor design has overcome both of these problems to a very large extent. The amount of output voltage which is fed back to the input side is negligible in modern transistors and h_re can be neglected and removed from the equivalent circuit. With modern transistors the graph of I_C versus V_CE is a horizontal line for voltages above about 1.5 volts. A horizontal line has a slope of zero and if h_oe is zero, the output resistance is infinity. An infinite output resistance means that the resistor representing h_oe may be removed from the circuit.

Figure 4.7 Simplified Equivalent Circuit.
For a verbal description click here.
The simplified equivalent circuit is shown in Figure 4.7. The equivalent circuit consists of the resistor labeled h_ie and the current source labeled i_b> h_fe. To make use of this circuit we must connect a couple of things to it. A Thevenin's equivalent circuit of a generator is connected to the B and E terminals. A load resistor is connected to the C and E terminals. We will use this circuit to derive the equations for gain and input impedance.
The current in the first loop is simply,
i_b = v_be / h_ie (4.14)
The output voltage is,
v_ce = - h_fe i_b R_L (4.15)
The minus sign in equation 4.15 arises from the fact that the current in the current source is flowing downward and so it is flowing upward in the load resistor. If we now substitute equation 4.14 into equation 4.15 and divide by v_be we obtain,
v_ce / v_be = - (h_fe R_L ) / h_ie (4.16)
If we define the voltage gain as A_V = v_ce / v_be then we have
A_V = - (h_fe R_L ) / h_ie (4.17)
The input impedance of a common emitter amplifier is equal to H_ie. The output impedance is virtually infinite.
Example 4.7

A BJT has the following parameters, h_fe = 90 and h_ie = 4 k ohms. If this transistor is placed in a circuit where the load resistance is 4.7 k ohms, what is the voltage gain of the circuit?

Solution:

A_V = - (h_fe R_L ) / h_ie = - ( 90 x 4.7 k ohms ) / ( 4 k ohms ) = 106
The solution to example 4.7 indicates that the amplifier in question will have an output voltage 106 times as large as its input voltage and the phase of the output signal will be inverted. 180 degrees phase shift.
Go back home.
Biasing the Bipolar Transistor.
The BJT is normally used to amplify small AC signals but it won't do anything unless it is provided with the proper DC voltages and currents. The process of providing the DC values is called biasing. One way to bias a transistor is as shown in Figure 4.2. The combination of V_BB and R_B will provide a constant DC current to the base. The collector current should be adjusted such that 1/2 of V_CC is dropped across R_C. V_CE will also be 1/2 of V_CC. This condition permits the AC output signal to be as large as it can possibly be. The collector voltage can "swing" from 0 to V_CC. This type of biasing is never used in practical circuits because the collector current depends on the value of the DC beta of the transistor. The value of beta changes with temperature and is different for different transistors even of the same type number.

Figure 4.8 Practical Audio Frequency Amplifier.
For a verbal description click here.
A complete practical one-stage audio frequency amplifier is shown in Figure 4.8. Approximately 2 volts DC are dropped across the emitter resistor which leaves a 10 volt range for V_CE (2 volts to 12 volts). The static collector voltage is halfway between 2 and 12, which is 7 volts. The voltage at the base is approximately 2.6 volts. Capacitor C₁ is necessary to prevent this voltage from interfering with the operation of or possibly even damaging the device which is to provide the signal to the amplifier. C₃ blocks the DC at the collector from reaching the circuits or devices which may be connected to the output of the amplifier. R₅ provides a charging path for C₃ to make sure that there is no DC voltage present at the output even though there is no other load connected. Remember back in chapter 2 when we were talking about mixtures of AC and DC? Well, here it is. The RC networks are used just as described to pass the AC while blocking the DC.
The purpose of C₂ requires a bit more explanation. If C₂ were not present, the gain of the amplifier would be considerably reduced. It works this way. When the input signal goes positive, the base current increases and so does the emitter current. That increases the voltage drop across the emitter resistor and reduces the effect of the increasing signal. The effect of the signal could not be completely canceled out because, if the change in emitter current were completely canceled out, there would be no change in emitter current to cancel out the change in base current. The effect of the changing input signal is considerably reduced, which considerably reduces the gain of the circuit. Connecting C₂ from the emitter to ground will prevent rapid changes in the emitter voltage and so the input signal will not have its effect reduced by any changes in the emitter voltage. The process of reducing the effective gain by removing the emitter bypass capacitor C₂ is called emitter degeneration and, as we will learn in the next chapter, is not necessarily a bad thing.
Go back home.
Operating Point Stability
The set of conditions, I_C, V_CE, etc., are referred to collectively as the operating point. The operating point of a transistor must be stabilized against two types of changes. 1) The temperature can change and the value of beta is very temperature dependent. 2) Changing transistors, transistors can and do burn out and have to be replaced. The replacement most likely will not have the same value of beta as the original unit. There is no guarantee that a circuit will always be operated at room temperature. Air conditioning and heating systems can break down; portable devices can be carried outside on a summer or winter day. A device which fails to operate if the temperature gets above 85degrees or below 65degrees will not be very useful. If a transistor burns out it must be replaced to restore operation. Even if the replacement transistor has the same number as the original transistor, its beta may differ by as much as 30% from the original. If the circuit is not properly designed, the circuit may not work following the replacement of a defective transistor.
If the circuit of Figure 4.2 were used as an amplifier (and it could be) it would suffer from both problems described above. The circuit of Figure 4.8 does not suffer from these problems and here is why. The base current is small compared to the current flowing down through R₁ and R₂. The voltage divider which is constituted by R₁ and R₂ is lightly loaded and its output voltage will change only slightly as the base current changes. Suppose that the collector current tries to increase due to a temperature or a transistor change. The emitter current is I_C + I_B and I_B is very much less than I_C; therefore, I_E is approximately equal to I_C. As I_C goes so goes I_E. I_E is trying to increase which will increase the voltage drop across R_E which, in turn, will increase the voltage at the emitter. The voltage divider of R₁ and R₂ is holding the voltage at the base almost constant. An increase of emitter voltage while the base voltage is held constant will cause the forward bias on the base-emitter junction to be decreased and, therefore, decrease the base current. Remember we started out with the emitter current trying to increase which led to a decrease in base current. A decrease in base current will counteract the original increase in collector (emitter) current and the increase will not be as great as it would otherwise be. In fact, the emitter current will change only very slightly. If the collector (emitter) current tries to decrease, the voltage across R_E will decrease, decreasing the emitter voltage while the base voltage is held constant. This increases the forward bias on the B-E junction and increases the base current which counteracts the decrease in collector (emitter) current.
If you were to set up the circuits of Figures 4.2 and 4.8 and put meters in the circuit to monitor the base and collector currents, you could see things happen. In the case of Figure 4.2 if heat were applied to the transistor the collector current would rise very rapidly. In the case of Figure 4.8 the collector current would change very slightly and the base current would drop off drastically. If the transistor were cooled, the currents would change in the opposite direction. A transistor with a higher beta will result in a larger collector current in the circuit of Figure 4.2 and a smaller base current in Figure 4.8.
The circuit of Figure 4.2 is called constant current biasing. It is never used in analog (as opposed to switching) circuits. The circuit of Figure 4.8 is called constant voltage biasing and it - or a variation of it - is used in all transistor circuits, including the internal circuitry of integrated circuits.
Go back home.
Circuit Analysis.
The circuit of Figure 4.8 is much easier to analyze if the voltage divider is replaced by its Thevenin's equivalent circuit as shown in Figure 4.9. Capacitors have been omitted because this is a DC analysis and capacitors are open circuits for DC. The values of V_BB and R_B are given by these equations
V_BB = V_CC R₂ / (R₁ + R₂) (4.18)
and
R_B = (R₁ R₂) / (R₁ + R₂) (4.19)
where R₁ and R₂ are the original base resistors as shown in Figure 4.8.

Figure 4.9 Thevenin's Equivalent Circuit Replaces R₁ and R₂
For a verbal description click here.
If equations 4.18 and 4.19 seem to have "come out of the blue," you need to review the section on Thevenin's equivalent circuit (section 1.3 pages 41 to 46).
We will now write the loop equations for the circuit of Figure 4.9. Summing voltages in the base loop gives
V_BB = R_B I_B + V_BE + R_E (I_B + I_C) (4.20)
The voltage drop across R_E (R₄ in Figure 4.8) is I_E R_E but I_E = I_B + I_C. The base current is given by
I_B = I_C / beta (4.21)
Substituting equation 4.21 into equation 4.20 and solving for IC gives
I_C = beta (V_BB - V_BE) / (R_B + R_E (1 + beta)) (4.22)
If beta is greater than 50 an error of less than 2% will be introduced by letting the (1 + beta) term in the denominator equal beta. Making this substitution and dividing through by beta we have
I_C = (V_BB - V_BE) / (R_E + R_B / beta) (4.23)
Equation 4.23 is probably the best one to use to calculate the collector current of a constant voltage biased BJT.
It is possible to make a further approximation but it must be applied with great care. In the denominator of equation 4.23 R_B / beta may be much less than R_E. If this is true the following equation may be used.
I_C = (V_BB - V_BE) / R_E if and only if R_B / beta << R_E. (4.24)

Example 4.8

Calculate the values of V_BB and R_B for the circuit of Figure 4.8.

Solution:

V_BB is the unloaded output of the voltage divider consisting of R₁ and R₂
V_BB = V_CC R₂ / (R₁ + R₂) = 12 v x 6.8 k ohms / (22 k ohms + 6.8 k ohms) = 2.83 v
R_B is the parallel combination of R₁ and R₂
R_B = R₁ R₂ / (R₁ + R₂) = 22 k ohms x 6.8 k ohms / (22 k ohms + 6.8 k ohms) = 5.19 k ohms

Example 4.9

If the transistor in Figure 4.8 has a beta of 150, what is the collector current?

Solution:

Which equation should we use? Equation 4.22 is the most exact form but the difference between beta and beta + 1 is only 0.66%. We might use equation 4.24 but that one is usually used only when beta is not given and a typical value must be assumed. We will use equation 4.23.
I_C = 2.83 v - 0.6 v / (1.8 k ohms + 5.19 k ohms / 150) = 2.23 v / (1.8 k ohms + 0.03 k ohms) = 1.22 mA.
If equation 4.24 had been used the error would have only been 1.67%, which is well within acceptable limits. Perhaps another example will illustrate when equation 4.24 should not be used.
Example 4.10

In a circuit similar to Figure 4.8 V_CC = 15 v, R₁ = 100 K ohms, R₂ = 47 k ohms, R₃ = 4.7 k ohms, R₄ = 3.3 k ohms and beta = 50. What is the collector current?

Solution:

Since beta = 50 this is a borderline case for the 2% rule but we will ignore beta + 1 and use equation 4.23. V_BB = 15 v x 47 k ohms / (100 k ohms + 47 k ohms) = 4.80 v and R_B = 100 k ohms x 47 k ohms / (100 k ohms + 47 k ohms) = 32.0 k ohms.
I_C = 4.80 v - 0.6 v / (3.3 k ohms + 32.0 k ohms / 50) = 4.20 v / (3.3 k ohms + 0.64 k ohms) = 1.07 mA.

Go back home.
The Common Collector (Emitter-follower) Amplifier.
If the collector of a BJT is placed at AC ground potential while the input signal is applied between ground and base and the output signal is taken between ground and emitter, the collector is common to input and output. Such an amplifier is a common collector configuration but is commonly known as an emitter-follower. An AC coupled emitter-follower is shown in Figure 4.10.

Figure 4.10 AC Coupled Emitter-follower.
For a verbal description click here.
The reason it is called an emitter-follower is because of that nearly constant 0.6 volt drop from base to emitter. How ever the base voltage may change, the emitter voltage is following along only 0.6 volts behind. To put it more precisely, for an NPN transistor the emitter voltage is 0.6 volts less then the base voltage. For a PNP transistor the emitter voltage is 0.6 volts greater than the base voltage. That 0.6 volts may not be important in the circuit of Figure 4.10 but in a DC coupled emitter-follower it may be very important.
The AC gain of an emitter-follower may be derived using the familiar common emitter parameters by drawing the equivalent circuit as in Figure 4.11. This circuit is a little difficult to follow (pun fully intended) and so the wires have been untangled in Figure 4.12. In equivalent circuits it is customary to omit DC biasing and capacitors because they add nothing to the AC circuit.

Figure 4.11 Common Collector Equivalent Circuit.
For a verbal description click here.

Figure 4.12 Figure 4.11 with Wires Untangled.
For a verbal description click here.
Writing a loop equation around the outside loop gives
v_in = i_b h_ie + v_o. (4.25)
We will make the approximation that the base current i_b is much less than the collector current i_c, and the emitter current will be considered equal to the collector current. The current flowing through R_L is the collector current h_fei_b and we have
v_o = i_b h_fe R_L. (4.26)
If we solve equations 4.25 and 4.26 for i_b and set them equal we have
v_o / (h_fe R_L) = (v_in - v_o) / h_ie (4.27)
Solving this equation for v_o / v_in and remembering that voltage gain is defined as v_o / v_in we have
A_V = h_fe R_L / (h_ie + h_fe R_L) (4.28)

Example 4.11.

A BJT has the following parameters, h_ie = 4 k ohms and h_fe = 100. In an emitter-follower with a load (emitter) resistor of 1 k ohms, what is the voltage gain?

Solution:

A_V = h_fe R_L / (h_ie + h_fe R_L) = 100 x 1 k ohm / (4 k ohms + 100 x 1 k ohm) = 0.962
The voltage gain of an emitter-follower is always slightly less than one. You may be wondering what use is an amplifier which slightly reduces the amplitude of the input signal. An emitter-follower has current gain. The current gain is equal to beta. For example, if you have a generator which can only supply 1 mA and you need to drive a load which requires 100 mA, an emitter-follower employing a BJT with a beta (or h_fe) greater than 100 will allow the generator to drive the load provided there are no other losses in the circuit.
Input Resistance.
The input resistance of an emitter-follower is
R_in = v_in / i_b (4.29)
If we rearrange equation 4.26 we have
v_o / i_b = h_fe R_L (4.30)
Because the gain of an emitter-follower is approximately unity, v_o = v_in. Combining this approximation with equations 4.29 and 4.30 we have
R_in = h_fe R_L (4.31)
The value of R_L is the parallel combination of all resistances connected from the emitter to ground.
Example 4.12.

In the circuit of Figure 4.13 an emitter-follower is being used to drive an 8 ohm speaker. If R₁ = R₂ = 390 ohms, R₃ = 15 ohms, beta = h_fe = 75 and h_ie = 5 ohms, what are (a) the voltage gain and (b) the input resistance?

Figure 4.13 Emitter-follower Driving a Speaker
For a verbal description click here.

Solution:

(a) The gain is given by equation 4.28. R_L in this equation is the parallel combination of R₃ and the 8 ohm speaker which is 5.22 ohms.
A_V = h_fe R_L / (h_ie + h_fe R_L = 75 x 5.22 ohms / (5 ohms + 75 x 5.22 ohms) = 0.987
(b) The input resistance is the parallel combination of the two 390 ohm resistors in the base circuit and the input resistance of the emitter-follower. The input resistance of the emitter-follower is given by equation 4.31.
R_in = h_fe R_L = 75 x 5.22 = 392 ohms
The total input resistance is the parallel combination of 390 ohms, 390 ohms and 392 ohms which is 130 ohms

Go back home.
Resistances in Parallel.
Some of you may be puzzled over why resistors are being treated as if they are connected in parallel when they are not connected to the same point in the circuit. If you are not puzzled, you may skip this section.
For example, the speaker and the 15 ohm resistor R₃ have been treated as if they are in parallel when it is obvious that there is a capacitor connected between them. We are talking about AC not DC. The job of the capacitor is to block DC and pass AC to the speaker. The value of the capacitor has been chosen such that its reactance is small at the lowest frequency to be passed to the speaker. The capacitor is essentially a short circuit for AC. When the capacitor is replaced by a short circuit the speaker and the 15 ohm resistor are in parallel.
The two 390 ohm resistors in the base appear more like they are in series than in parallel. The AC signal is applied to the junction of the two resistors. One of the resistors goes to ground and the other one goes to the power supply (V_CC). Within the power supply is a large capacitor connected from V_CC to ground, or a voltage regulator, most likely both. For AC there is a short circuit connected from V_CC to ground, which means that connecting a resistor to V_CC is the same as connecting it to ground as far as AC is concerned. The input resistance of the transistor appears from base to ground and so is in parallel with the resistors in the base circuit.
Go back home.
Output Resistance.
To determine the output resistance of an emitter- follower we rearrange the equivalent circuit of Figure 4.12 and redraw it in Figure 4.14.

Figure 4.14 Measuring Output Resistance of Emitter-follower.
For a verbal description click here.
The generator has been removed from the input and replaced by its internal resistance R_g. The load resistor has been removed and a generator has been connected to the output. The purpose of this is to apply a known voltage to the output and see how much current flows.
This can be done in the laboratory if care is taken not to drive the transistor into nonlinear regions of its I-V characteristic.
Summing the voltage drops around the outside loop gives
i_b (R_g + h_ie) = V. (4.32)
The current flowing in the generator is
I = i_b (h_fe + 1). (4.33)
Eliminating i_b between equations 4.32 and 4.33 and rearranging yields
V / I = (R_g + h_ie) / (h_fe + 1) (4.34)
Since R_O = V / I we have
R_O = (R_g + h_ie) / (h_fe + 1) (4.35)

Example 4.13.

In the circuit of Figure 4.13 calculate the output resistance which is effectively connected across the speaker. The output resistance of the generator is 50 ohms.

Solution:

The output resistance at the emitter of the transistor is given by equation 4.35. R_g must be the parallel combination of the generator resistance and the two resistors in the base circuit, 50 ohms in parallel with two 390 ohm resistors, which is 39.8 ohms
R_O = (R_g + h_ie) / (h_fe + 1) = (39.8 ohms + 5 ohms) / (75 + 1) = 0.589 ohms
The true output resistance is R_O in parallel with 15 ohms but it isn't going to make much difference.
R_out = 15 ohms x 0.589 ohms / (15 ohms + 0.589 ohms) = 0.567 ohms.

Go back home.
Determining Transistor Parameters.
Transistor parameters may be found in a data sheet for the particular transistor or in a transistor data book. Data sheets for individual transistors may be obtained from the manufacturer often free of charge or for a nominal fee. These data sheets give all of the information you could possibly want. Data sheets give a range of values for each parameter. Whether you use an average value or the minimum value will depend on what you are trying to do.
Most data books do not give a value for h_ie at all. They usually give a range of values for the current gain. For audio frequencies the values of beta and h_fe are the same. It is unusual for a data book to give a value of h_fe at high frequencies.
If you need to know the value of h_ie and you can't find it anywhere you can estimate it. H_ie = 25 mv / I_B. Since I_B = IC / beta h_ie can be estimated as
H_ie = 25 mv x beta / I_C (4.36)
Whoa! What happened to 4.4, 4.5, and 4.6? They are about FETs and can be found on the FETs page.
Go back home.
4.7 Differential Amplifier.
In the next chapter we will take up the study of operational amplifiers. A very important aspect of the op amp is its differential or difference input. A differential input consists of two input points with respect to ground. The circuit subtracts the two input signals. Thus the output of a differential amplifier is
V_O = A_V (V₂ - V₁) (4.37)
where A_V is the voltage gain of the amplifier, V₁ is the signal applied to the noninverting input and V₂ is the signal applied to the inverting input.
The noninverting input is so named because an AC signal applied to this input is not inverted in phase. The inverting input is so named because an AC signal applied to this input is inverted in phase.

Figure 4.34 BJT Differential Amplifier.
For a verbal description click here.
Figure 4.34 shows a differential amplifier using BJTs. Q₁ and Q₂ work together to form the differential amplifier. Transistor Q₃ along with R₇, R₈ and R₉ form a constant current sink for the emitters of Q₁ and Q₂. The resistor network consisting of R₇ and R₈ keeps the voltage at the base of Q₃ very stable regardless of changes in the base current of Q₃. A very stable base voltage means that the emitter current will also be very stable and the collector current will also be very stable. Q₃ carries the sum of the emitter currents of Q₁ and Q₂. If the emitter current in Q₁ changes by a certain amount I, the emitter current of Q₂ must change by an amount equal in magnitude and opposite in sign -I. This helps to maintain equal amounts of gain for both inputs.
Resistors R₅ and R₆ introduce emitter degeneration in Q₁ and Q₂, which lowers and further equalizes the gains. In an amplifier of this type emitter degeneration is not a bad thing. The gain is set by the ratio of R₃ to R₅ rather than the parameters of the transistors. It should be noted that R₃ = R₄ and R₅ = R₆. If maximum gain is desired resistors R₅ and R₆ may be replaced by pieces of wire but Q₁ and Q₂ must be very closely matched (have identical parameters) if the gains from the two inputs are to be equal in magnitude.
The output may be taken in either one of two ways. Output 1 is taken between the collectors of Q₁ and Q₂ as shown. This is a differential or as it used to be called a push-pull output. It is suitable for driving another differential amplifier or a balanced transmission line. Some oscilloscopes employ differential amplifiers from beginning to end. The deflection plates of a CRT must be driven from a differential output for best performance.
Output 2 is taken between the collector of Q₁ and ground. The input marked with a - sign is the inverting input. A positive-going signal applied to the base of Q₁ will cause its collector current to increase. That increase will cause a larger voltage drop across R₃ which will cause the voltage at the collector of Q₁ to decrease. The input marked with a + sign is the noninverting input. A positive- going signal applied to the base of Q₂ will cause the collector current of Q₂ to increase. That increase in collector current of Q₂ must be mirrored by a decrease in the collector current of Q₁. A decrease in the collector current of Q₁ will cause the drop across R₃ to decrease. The decreased voltage drop across R₃ will increase the voltage at the collector of Q₁. In case you forgot, we started with an increase in the input voltage which shows that the input marked with a + sign is the noninverting input.
Problems

The collector current of a BJT begins in the emitter, flows through the base region and ends up in the collector region. (This current refers to charge carrier current, not conventional current.) What kind of charge carriers (minority or majority) make up the collector current when it is in the (a) emitter region, (b) the base region, and (c) the collector region?

In a PNP transistor the base current (conventional current) flows out at the base terminal. Where does it flow in?

In the circuit of Figure 4.3 the values are as follows: V_CC = 28 volts, beta = 150, V_{IN_ON} = 5 volts, V_{IN_OFF} = 0 and R_B = 8.2 k ohms. (a) If the lamp current is 65 mA, will the lamp be turned fully on? (b) After a few years the lamp burns out and someone replaces it with a lamp which draws 100 mA. Will this new lamp be fully turned on by the BJT switch? What will be the lamp current?

In the circuit of Figure 4.4 V_{IN_ON} = 10 volts and V_{IN_OFF} = 2 volts. R₁ = 3.3 k ohms and R₂ = 820 ohms. All other circuit parameters are as shown in the figure. Is the switch on when the control signal is high and off when the control signal is low? Show detailed calculations for both off and on states.

For the starting conditions of problem 4, all of the students involved with designing and building the circuit have graduated. The transistor burns out and the equipment must be repaired because someone is giving a paper next week. Someone finds an old germanium transistor in a drawer and in desperation installs it in the circuit. The replacement has a beta of 100 but V_BE to turn it on is 0.15 volts. Is the switch on when the control signal is high and off when the control signal is low? Show detailed calculations for both off and on states.

For the starting conditions of problem 4, all of the students involved with designing and building the circuit have graduated. The transistor burns out and the equipment must be repaired because someone is giving a paper next week. Someone finds an old transistor in a drawer and in desperation installs it in the circuit. The replacement transistor is a silicon unit but its beta is 25. Is the switch on when the control signal is high and off when the control signal is low? Show detailed calculations for both off and on states.

A transistor has the following parameters, h_ie = 2.5 k ohms and h_fe = 85. If R_L = 3.3 k ohms what is the gain of the common emitter amplifier?

Figure 4.36 Common Emitter and Emitter-follower Amplifier.
For Q₁, h_ie = 2 k ohms and h_fe = beta = 120.
For Q₂, h_ie 30 ohms and h_fe = beta = 55.

For a verbal description click here.

Calculate the value of the collector current of Q₁ in the circuit of Figure 4.36. Do not use an equation which is any more complicated than necessary.

Calculate the value of the collector current of Q₂ in the circuit of Figure 4.36. Do not use an equation which is any more complicated than necessary.

Calculate the voltage gain of the emitter-follower stage in Figure 4.36. Remember to take everything into account when determining RL.

Calculate the voltage gain of the common emitter stage in Figure 4.36. Remember to take everything into account when determining RL.

The input resistance of a common emitter amplifier is equal to h_ie. What is the input resistance of the circuit of Figure 4.36?

In the circuit of Figure 4.36 if the 75 ohm load were removed, what would be the output resistance of the circuit?

In the circuit of Figure 4.34 the collector current of Q₃ is 1 mA. If the collector current of Q₁ is 0.340 mA, what is the collector current of Q₂?

If the gain of a differential amplifier is 10, V1 = +1.0 volt and V2 = +1.0 volt, what is the output voltage?

If the gain of a differential amplifier is 100, V1 = +1.00 volt and V2 = +1.01 volt, what is the output voltage? Be sure to give sign as well as magnitude.

If the gain of a differential amplifier is 100, V1 = +1.01 volt and V2 = +1.00 volt, what is the output voltage? Be sure to give sign as well as magnitude.

If the gain of a differential amplifier is 100, V1 = -1.00 volt and V2 = -1.01 volt, what is the output voltage? Be sure to give sign as well as magnitude.

If the gain of a differential amplifier is 100, V1 = -1.01 volt and V2 = -1.00 volt, what is the output voltage? Be sure to give sign as well as magnitude.

Answers to problems.

Part a, majority. Part b, minority. Part c, majority.
At the emitter.
Part a, required base current = 0.433 mA, supplied base current = 0.536. Lamp is fully on. Part b, required base current = 0.667 mA. The lamp is not fully on. Lamp current = 80.4 mA.
On state. Required I_B = 0.793 mA. Supplied I_B = 2.12 mA. Switch is on. Off state. V_BE unloaded = 0.398 V. Switch is off.
On state. Required I_B = 0.793 mA. Supplied I_B = 2.80 mA. Off state. V_BE unloaded = 0.398 V. BE is forward biased. Supplied I_B = 0.378 mA. The switch will be between the on and off states.
On state. Required I_B = 3.17 mA. Supplied I_B = 2.12 mA. The switch is not fully on. Off state. Same as in problem 4.
A_V = 112.
I_C = 1.20 mA by equation 4.24.
I_C = 47.2 mA by equation 4.23.
A_V = 0.987.
A_V = 43.6. Hint: There are 4 components that have to be added in parallel to make up R_L.
R_in = 1.57 k ohms.
R_O = 16.4 ohms.
I_{C_Q2} = 0.660 mA.
V_O = 0 V.
V_O = + 1.00 V.
V_O = - 1.00 V.
V_O = - 1.00 V.
V_O = + 1.00 V.