Chapter 3.
Power Supply Circuits.3.4 Semiconductor Diodes.
Before we can discuss rectifier circuits it is necessary to understand the semiconductor diode. An ideal diode is a device which will conduct current in one direction only. When current flows in the forward direction, the resistance of the diode is zero, the voltage drop is zero. When current attempts to flow in the reverse direction it encounters an infinite resistance. Absolutely no current will flow and the voltage can build up to any value demanded by the circuit. As with all other ideal things, the ideal diode does not exist in the real world but real diodes come close enough to be most useful.Unfortunately, there is insufficient space here to cover the physics of semiconductors in detail. Whole books 1 have been devoted to this topic and there is a course in this department entitled "Solid State Physics" which interested students should enroll in. Meanwhile, we can only scratch the surface. Emphasis will be placed on visualization of the physical processes which are taking place.
1 Semiconductor Devices and Applications by R. A. Greiner McGraw-Hill 1961
A Semiconductor Is a Semiconductor Is a Semiconductor.
A semiconductor is not a very good conductor nor is it a very good insulator. It is a semiconductor. Two examples of semiconductor material are silicon and germanium.Silicon and germanium each have 4 valance electrons in an outer shell which has room for 8 electrons. These elements (and carbon as well) form very stable tetrahedral crystals with the shared valance electrons filling the outer electron shell of each atom. If every electron stayed in place within the crystal lattice the crystal would be a perfect insulator. The electrons do not stay home.
Figure 3.3 shows the possible energy levels for the electrons in a semiconductor crystal. When the electrons have a low energy level, they are in the valence energy band. Electrons which fall within this energy band will be bound to their particular valence bond. If an electron is given enough energy to jump over the forbidden energy band and enter the conduction band, it is set free from the valence bond and can move through the crystal. 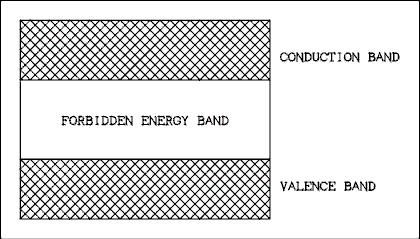
Figure 3.3 Energy Diagram of a Semiconductor Material.
For a verbal description click here.
The width of the forbidden band is called the band-gap energy. The band-gap energy for silicon at room temperature (300 degrees K) is 1.106 electron-volts (ev) and for germanium it is 0.67 ev. At room temperature there is enough thermal energy in the crystal lattice to promote some electrons to the conduction band.
Holes and Electrons.
Electrons which are in place in the lattice are in the valence energy band. Due to normal thermal agitation an electron can gain enough energy to move into the conduction band and leave its place in the lattice to become a conduction electron. An electron which has been promoted into the conduction energy band is free to move through the crystal under the influence of an electric field. But there is more to conduction in a semiconductor than conduction electrons.When an electron leaves its place in the crystal lattice it leaves behind a hole in the lattice. Strange as it may seem, the hole does not stay in place but moves as if it were a positively charged particle. It has energy and even momentum. A hole can move by a nearby valence electron jumping from its place in the crystal lattice to the hole without entering the conduction energy band. After the electron has jumped, it leaves a hole where it used to be. Thus, the hole can move through the crystal lattice.
Thermal energy in the crystal lattice creates hole- electron pairs which move through the crystal. If there is an electric field present, the electrons will move toward the positively charged region and the holes will move toward the negatively charged region. If there is no electric field present, the holes and electrons will move randomly.
If you visualize a crystal of silicon warming up from absolute zero, hole-electron pairs will begin to form. This process cannot continue indefinitely or the crystal would come apart because all of its valence bonds would be broken. When holes and conduction electrons (electrons not held in a valance bond) become plentiful enough, electrons will begin to fall into holes they happen to run into. This process is called recombination and goes on at the same rate as hole- electron pair formation. The equilibrium between pair formation and recombination causes silicon and germanium crystals to be semiconductors at room temperature.
In pure semiconductor material the concentration of holes is the same as the concentration of electrons in the conduction band. (The total number of electrons cannot change, what we mean when we talk about changing the concentration of electrons, is the number of electrons which are free for conduction.) In pure silicon or germanium
Ne = Nh = KS T(3/2) (3.1) where Nh is the concentration of holes, Ne is the concentration of electrons in the conduction band, KS is a constant which must be determined experimentally and T is the Kelvin temperature. The value of KS is 4.74 x 1022 for silicon and 1.76 x 1022 for germanium. Ne and Nh have units of 1/m2.We may now define the intrinsic charge carrier concentration ni as
Ni = KS T(3/2) (3.2) Equations 3.1 and 3.2 say that the charge carrier concentration is quite temperature dependent. Equation 3.2 defines the pure semiconductor or intrinsic charge carrier concentration.Changing the Relative Concentration of Holes and Electrons.
Now suppose that we deliberately add some impurities to a crystal of pure semiconductor such as silicon. We are not going to just throw in some dirt from the floor; we will carefully control what goes in and how much.If we add an element from group 5 in the periodic table the effect on a semiconductor is striking. The elements from group 5 have five electrons in the outer shell. Wherever one of these atoms appears in the crystal lattice, four of its outer electrons go into valence bonds and the fifth one becomes very loosely bound to its atom. A very small amount of energy (about 0.05 ev) is needed to promote this electron into the conduction band. Such an impurity is called a donor impurity because each atom donates an electron to the conduction energy band.
If we go back to pure silicon and add an element from group 3 in the periodic table the effect on a semiconductor is opposite to that for an element from group 5. The elements from group 3 have three electrons in the outer shell. Wherever one of these atoms appears in the crystal lattice, there are only three electrons in the outer shell to go into valence bonds. The unfilled valence bond is a hole. Once a wandering electron has fallen into this hole, a comparatively large amount of energy is required to promote that particular electron back into the conduction energy band. That electron and its three companions will remain in place and a hole will have been set free to wander through the crystal lattice. Such an impurity is called an acceptor impurity because each atom accepts an electron from the conduction energy band and causes a conduction hole to be created.
When a donor impurity loses its loosely-bound electron or an acceptor impurity captures a wandering electron (loses its loosely-bound hole), the impurity atom is said to be ionized. Ionization in a solid means the same thing it means in a liquid or gas, the loss of, or gain of an extra electron. When an impurity is added to a semiconductor, most of the impurity atoms are ionized most of the time, statistically speaking.
Because the impurity atoms are virtually 100 percent ionized, for every atom of donor impurity there is an additional electron in the conduction band. For every acceptor atom added, there is an additional conduction hole in the crystal. The meaning in this discussion is that donor impurity is added to one piece of semiconductor and acceptor impurity is added to another piece of semiconductor.
Recombinations occur when wandering holes and wandering electrons happen to collide. The probability of collisions goes up as the concentration of either holes or electrons goes up. When, for example, a donor impurity is added to a semiconductor, the increased concentration of electrons causes more frequent collisions and a higher rate of recombination. The recombination rate falls again when the hole concentration has been reduced to the point where a new equilibrium has been established. The end result is to decrease the concentration of holes in the crystal. It can be shown mathematically, in about ten pages, note 1, that
Ne Nh = ni2 (3.3) where Nh is the concentration of holes, Ne is the concentration of electrons and ni is as defined in equation 3.2. Because the impurity atoms are completely ionized, the concentration of electrons is equal to the concentration of donor atoms Ne = Nd and for acceptor impurity Nh = Na where Nd and Na are the concentrations of donor and acceptor impurity atoms respectively. Thus it is possible to write for a semiconductor which has been "doped" with a donor impurityNe = Nd and Nh = ni2 / Nd (3.4) and for a semiconductor "doped" with an acceptor impurityNh = Na and Ne = ni2 / Na (3.5) Some Terms to Be Remembered.
As you may have guessed the process of adding impurity atoms to a semiconductor crystal is called doping. A semiconductor which has been doped with a donor impurity has many more negative charge carriers than positive charge carriers. This is known as N (negative) type semiconductor. A semiconductor which has been doped with an acceptor impurity has many more positive charge carriers than negative charge carriers. This is known as P (positive) type semiconductor.There are two types of charge carriers, holes and electrons. A majority carrier is the type of carrier which there are more of in a particular type (P or N) of semiconductor. A minority carrier is the type of carrier which there are fewer of in a particular type (P or N) of semiconductor.
Example 3.2
Identify each of the following as majority or minority carriers: (a) electrons in N type semiconductor, (b) holes in P type semiconductor, (c) electrons in P type semiconductor and (d) holes in N type semiconductor. Solution:
The majority carriers have the same charge polarity as the type of semiconductor in which they are found. The one which is left is the minority carrier. Thus, (a) majority, (b) majority, (c) minority and (d) minority. The P-N Junction
Figure 3.4a shows a schematic representation of two blocks of semiconductor material. The block on the left is N type and the dots represent conduction electrons. The block on the right is P type and the circles represent the conduction holes. The concentration of minority carriers is so small as to be negligible at room temperature. In Figure 3.4b the two blocks of semiconductor material have been placed in physical contact. * As soon as contact has been established, the normal wanderings of charge carriers due to thermal agitation will cause some charge carriers to cross the junction. As soon as a carrier crosses the junction itbecomes a minority carrier. The probability of colliding with a carrier of opposite sign is very high and the wanderer will soon disappear by recombination with a carrier of opposite sign. There is a net movement of charge across the junction with electrons moving to the right and holes moving to the left. The departed electrons on the left leave behind the ionized donor impurity atoms which have a positive charge. The departed holes on the right leave behind the ionized acceptor impurity atoms which have a negative charge. That places an electric field across the junction, which is positive on the left and negative on the right. This electric field eventually builds up to such a value as to prevent any more electrons from moving to the right or holes from moving to the left across the junction. The graph in Figure 3.4b indicates the electric potential within the block of semiconductor material. The electric potential comes to zero at each end of the block; if it did not, we would have a cheap source of electricity. 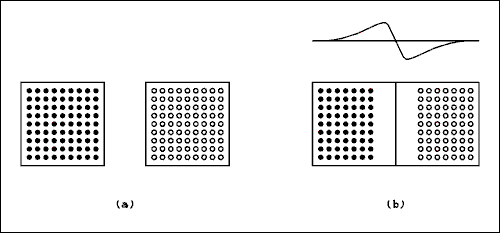
Figure 3.4 "Making" a P-N Junction Diode
For a verbal description click here.
* This is not how P-N junction diodes are manufactured.
In fact, this could not even be done in the laboratory.
This is merely a thought experiment which illustrates how the
depletion region and contact potentials are formed in a P-N junction.
The region near the junction becomes depleted of charge carriers in the conduction band. As stated above, there are ions in the depletion region but these ions are held in the crystal lattice and are not in the conduction energy band. The depletion region constitutes an insulator and the regions on either side of the depletion region which are not depleted of charge are conducting regions. This concept is very important. Failure to understand the depletion region will result in failure to understand how P-N junctions conduct in only one direction.
Animation, which is not possible in a paper book could not be done in any medium when I was teaching this subject. We have sure come a long way baby.
When the two pieces of semiconductor touch, the electrons from the N side and the holes from the P side start to randomly wander across the junction. The animation shows holes and electrons making a beeline toward their opposite number on the other side. Randomness is much harder to do in animation so the much easier straight line path was taken. It cannot be over emphasized that when electrons and holes meet and mutually annihilate, nothing is being destroyed. The electrons remain in existence but their energy level has been reduced so they are no longer in the conduction energy band. The electron filled a hole so it no longer exists but it was never their in the first place. 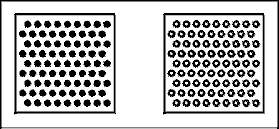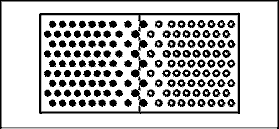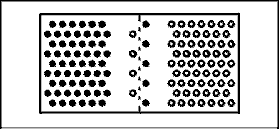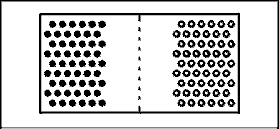
Figure 3.4c Animation showing Figure 3.4a and 3.4b in action.
For a verbal description click here.
Figure 3.5a shows a P-N junction with an external battery connected in such a polarity as to increase the potential across the junction. The effect of this is to increase the width of the depletion region and increase the potential across the junction. Notice that the positive terminal of the battery is connected to the N type semiconductor and the negative terminal of the battery is connected to the P type semiconductor. This condition is known as reverse bias. Under normal conditions no appreciable current will flow through a reversed biased P-N junction. It is true that minority carriers on the left (holes) are moving to the right across the junction and minority carriers on the right (electrons) are moving to the left across the junction. In modern P-N junction diodes this minority carrier current is so small that an electrometer is required to measure it. 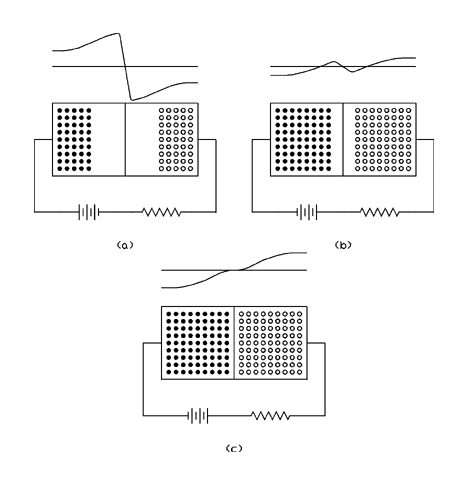
Figure 3.5 Reversed and Forward Biased P-N Junction
For a verbal description click here.
In the animation it appears that the electrons on the left and the holes on the right are being absorbed by the end lines. On the left the electrons are being absorbed into the copper wire that makes contact with the semiconductor and sucked into the positive terminal of the battery. On the right there are electrons coming from the negative terminal of the battery and fed into the semiconductor. At the point of contact between the semiconductor and copper, electrons are combining with holes. The current will flow only when the voltage is changing. This is like a capacitance and is called the "charge storage capacitance", or "charge storage effect", of the diode. 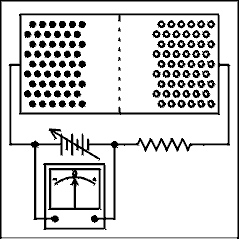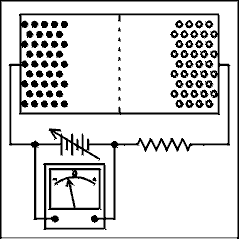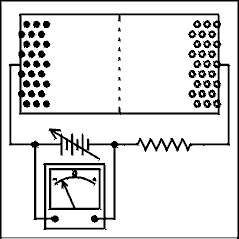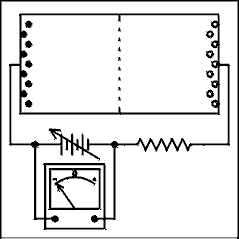
Figure 3.5d Figure 3.5a in action.
For a verbal description click here.
The depletion region constitutes an insulator and the regions where there are charge carriers in the conduction energy band are conductors. This forms a capacitor. As the voltage changes the width of the depletion region changes, changing the amount of capacitance. Any P-N junction will show varying amounts of capacitance as the reverse voltage is changed. In rectifiers and small switching diodes this is only a few picofarads. Special diodes are available that have enhanced capacitance and are known as variable capacitance diodes or varicaps for short.
Figure 3.5b shows a P-N junction which is slightly forward biased. The first few tenths of a volt only serve to reduce the potential gradient across the junction and no conduction results. In Figure 3.5c the forward bias has been increased to the point where the contact potential has been overcome. The width of the depletion region has been reduced to zero, and current now flows in the forward direction. Notice that the positive terminal of the battery is connected to the P type semiconductor and the negative terminal of the battery is connected to the N type semiconductor. This condition is known as forward bias.
A forward biased P-N junction will conduct large amounts of current at a voltage drop of less than one volt. As the current is increased in the forward direction, the voltage increases logarithmically as shown in Figure 3.6. 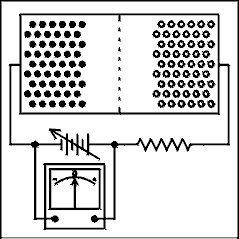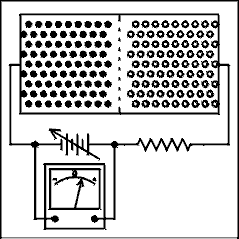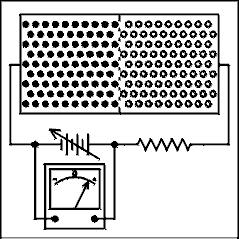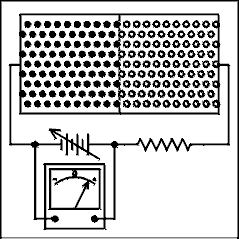
Figure 3.5e Figures 3.5b and c in action.
For a verbal description click here.
The reverse bias on a P-N junction cannot build up to infinity. As the reverse bias voltage is increased, the electric field across the junction becomes so great as to rip electrons out of their valence bonds. The electric field imparts enough energy to valence electrons to promote them to the conduction energy band. The result is that we have a new source of conduction electrons. The newly freed electrons are accelerated to a high velocity and when they collide with other valence electrons, these valence electrons are also promoted to the conduction energy band. The current rises to a very large value and the voltage cannot rise any further. This condition is called avalanche breakdown but is sometimes mistakenly called Zener breakdown. Zener breakdown will be covered in a later section. Avalanche breakdown places a practical limit on how much voltage a P-N junction diode can withstand in the reverse biased direction. 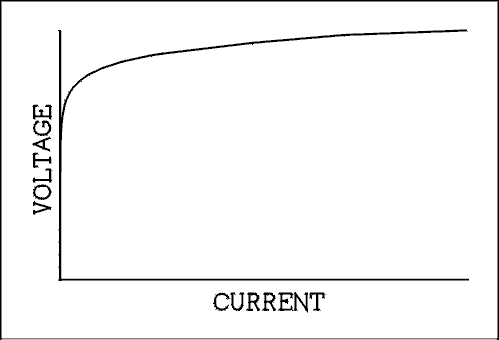
Figure 3.6 Voltage Versus Current Curve of a P-N Junction
For a verbal description click here.
A Derivation.
Get in touch with your inner physicist.
In the discussion above it was said that electrons from the N side of the junction will move towards the P side of the junction. We will call this current INN(0). The first subscript gives the polarity of the charge carrier and the second gives the type of semiconductor where the charge carrier originated. The "(0)" means with zero external bias applied. It can be shown that (note 1)INN = INN(0) e-(eVd/kT) (3.6) andIPP = IPP(0) e-(eVd/kT) (3.7) Under zero bias conditions there can be no net flow of holes or electrons across the junction; therefore,INN = INP and IPP = IPN That is to say there is an equilibrium of charge carriers so that the number of minority electrons crossing from P to N is equal to the number of majority electrons crossing from N to P. The same goes for holes. This means thatINP(0) = INN(0) e-(eVd/kT) (3.8) AndIPN(0) = IPP(0) e-(eVd/kT) (3.9) The "e" in the exponent is the charge on the electron, Vd is the diffusion voltage, k is Boltzmann's constant and T is the Kelvin temperature. If an external bias Vj is applied, these equations becomeINN = INN(0) e-e(Vd-Vj)/kT (3.10) AndIPP = IPP(0) e-e(Vd-Vj)/kT (3.11) With an external bias applied the total junction current isIJ = holes from P to N + electrons from N to P Combining this equation with equations 3.8 and 3.9 we haveIJ = (INN + IPP) e-e(Vd-Vj)/kT - IPN(0) - INP(0) (3.12)
IJ = ( INP(0) + IPN(0) ) (eeVj/kT - 1) (3.13) If we let IO = INP(0) + IPN(0) we haveIJ = IO (eeVj/kT - 1) (3.14) This is the "diode equation" and its derivation is obligatory in any discussion of semiconductor diodes.For negative values of Vj (reverse bias) the limiting case is IJ = IO. IO is correctly called the reverse saturation current but is often called the reverse leakage current. For modern silicon P-N junction diodes the value of IO is of the order of 10-12 amperes.
For positive values of Vj the current will rise exponentially. Diodes are never used in circuits where the circuit determines the voltage. Diodes are used in circuits where the circuit sets the current and the diode itself is allowed to set its own voltage drop. With current as the independent variable the voltage rises logarithmically and will easily stay within realistic bounds.
CONGRATULATIONS!
If you made it through the above you deserve some kind of reward. Turn off your computer and go do something that's fun.