Inicialmente, consideraremos forças distribuídas
![]() de módulo proporcional ao elemento de área
de módulo proporcional ao elemento de área
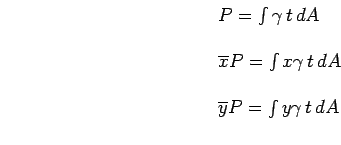 no qual elas atuam e que variam linearmente com a distância de
no qual elas atuam e que variam linearmente com a distância de
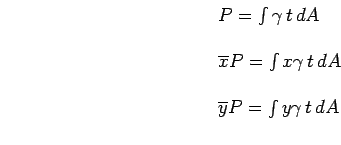 a um determinado eixo polar.
Um caso clássico que ilustra esse problema é o de uam seção transversal de uma viga sujeita a flexão pura, uma
vez que demonstra-se em Resistência dos Materiais que as forças internas em qualquer seção da viga são forças
distribuídas, cujos módulos
a um determinado eixo polar.
Um caso clássico que ilustra esse problema é o de uam seção transversal de uma viga sujeita a flexão pura, uma
vez que demonstra-se em Resistência dos Materiais que as forças internas em qualquer seção da viga são forças
distribuídas, cujos módulos
 variam linearmente com a distância
variam linearmente com a distância
![]() a partir
de um eixo passando pelo centróide da seção. Esse eixo, é conhecido como eixo neutro da seção, de modo que
as forças de um lado do eixo neutro são de compressão, e do outro lado são forças de tração, e sobre o
eixo neutro as forças são nulas.
a partir
de um eixo passando pelo centróide da seção. Esse eixo, é conhecido como eixo neutro da seção, de modo que
as forças de um lado do eixo neutro são de compressão, e do outro lado são forças de tração, e sobre o
eixo neutro as forças são nulas.
O módulo da força resultante
![]() é igual a soma dos módulos das forças elementares
é igual a soma dos módulos das forças elementares
![]() sobre a seção
inteira, portanto:
sobre a seção
inteira, portanto:
A integral
![]() que aparece na Equação (7.1) é conhecida como sendo o momento de primeira ordem
da seção em relação ao eixo
que aparece na Equação (7.1) é conhecida como sendo o momento de primeira ordem
da seção em relação ao eixo
![]() . Portanto sabemos que:
. Portanto sabemos que:
E como o eixo neutro coincide com o eixo
![]() , temos que
, temos que
![]() , e portanto a força resultante que
atua sobre a seção é nula, restando apenas o momento resultante que atua sobre o eixo neutro. Para calcular
o valor do momento tomemos um elemento
, e portanto a força resultante que
atua sobre a seção é nula, restando apenas o momento resultante que atua sobre o eixo neutro. Para calcular
o valor do momento tomemos um elemento
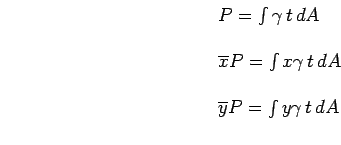 , distante
, distante
![]() do eixo neutro. Para esse elemento, o momento
de
do eixo neutro. Para esse elemento, o momento
de
![]() em relação ao eixo neutro é dado por:
em relação ao eixo neutro é dado por:
Portanto, para obter o momento resultante
![]() que atua sobre a seção, basta somar todos os
que atua sobre a seção, basta somar todos os
![]() que atuam
sobre a seção, assim, teremos que:
que atuam
sobre a seção, assim, teremos que:
A integral
![]() que aparece na Equação (7.2) é conhecida como momento de sgunda ordem ou momento
de inércia de uma seção em relação ao eixo
que aparece na Equação (7.2) é conhecida como momento de sgunda ordem ou momento
de inércia de uma seção em relação ao eixo
![]() , e é matematicamente representado por
, e é matematicamente representado por
![]() . É interessante notar
que
. É interessante notar
que
![]() será sempre positivo, uma vez que a área e
será sempre positivo, uma vez que a área e
 serão sempre positivos.
serão sempre positivos.
Do mesmo modo que definimos o momento de segunda ordem em relação a
![]() , podemos definir o momento de segunda ordem
em relação ao eixo
, podemos definir o momento de segunda ordem
em relação ao eixo
![]() , e desse modo teremos:
, e desse modo teremos: