Fonctions appliquées plus spécifiquement au calcul différentiel et intégral avancé (maths 303 ou EEE)
La structure d'un graphique en 3D (toujours ouvrir la bibliothèque with(plots):)
|
plot3d(f(x),x=a..b, y=c..d) |
Sur le même modèle que le graph en 2D; toutes les options du 2D s'appliquent au 3D. |
Options spécifiques au 3D
|
axes= boxed, normal, frame, none |
boxed: le graph est pris dans un cube dont les arêtes sont les axes; normal: les axes i, j, et k se croisent à l'origine ; frame: les axes i et j forment une boîte et k s'élève perpendiculaire à ce plan ; none: (par défaut) sans axes |
|
view=zmin..zmax ou view=[xmin..xmax , ymin..ymax, zmin..zmax] |
Différentielles (on doit toujours ouvrir la bibliothèque with(DEtools): pour utiliser les différentielles)
| D[a$n,b$n,c$n](fonction)(variables) | ex: pour dériver la fonction f:=(x,y,z)->x3y2+4x-9y2-x8y6z2
par rapport à y, puis x et finalement par rapport à z deux fois Maple associe un chiffre à chacune des variables dans l'ordre où elles apparaissent; ainsi, ici, x:1, y:2, z:3. Nous utiliserons ces chiffres dans les crochets (à la place des lettres a,b,c) pour donner l'ordre dans lequel Maple doit dériver. La position a est celle que Maple dérivera en premier et ainsi de suite...Le nombre n nous après le $ nous dit combien on doit dériver de fois par rapport à cette variable. Pour notre exemple, nous devrons donc écrire D(2,1,3$2)(f)(x,y,z) |
Solutionner des équations différentielles (Maple n'est pas très efficace pour effectuer cette tâche; ne vous surprenez donc pas d'obtenir des réponses bizarres pour quelque chose qui devrait être très simple). Voir la section dans Commandes plus spécifiquement appliquées au calcul intégral.
Pour trouver les points critiques d'une fonction (fonction à 2 variables seulement): Maple va tracer des cercles autour des maximum et des minimum et "s'éloigner" des points de selle. Comme une image vaut mille mots...
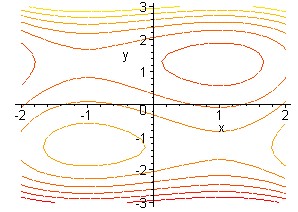On
aurait ici des max ou min dans les 1er et 3ème quadrants
et des points de selles dans les 2ème et 4 ème
quadrants.
Cette fonction est surtout utile pour vérifier les réponses que l'on obtient
par le test de la dérivée seconde
| contourplot(f(x,y),x=a..b, y=c..d, contours=n) | de la même façon que le plot normal. la valeur n donne le nombre de contours (lignes) que Maple tracera. Si on ne voit pas de cercles se former et qu'on est sûrs qu'il y a un point critique, augmenter le n de contours ou diminuer l'intervalle en x ou en y) |
Les coordonnées polaires (on définit les points par (r,t) où r est le
rayon et t l'angle theta en radians)
Graphique polaire
| polarplot(r,t=a..b); | on utilise souvent l'option scaling=constrained pour avoir un graphique 1:1 |
Intégrales doubles (pas vraiment plus compliqué)
dans l'ordre dxdy
| int((int(f(x,y),x=g(y1)..g(y2))),y=a..b ); | où g(y1) et g(y2) sont des fonctions de y, les bornes de x |
dans l'ordre dydx, on inverse x et y et on mets les bornes de y par rapport à x
