Princípio dos Trabalhos Virtuais

Admitamos a existência de um ponto material sujeito a ação de várias forças, como é apresentado na Figura 9.1. Admitamos ainda que este ponto material é deslocado do ponto A para o ponto A', descrevendo um deslocamento $\delta_r$.

Figure 9.1: Ponto material sujeito a várias forças e com deslocamento virtual

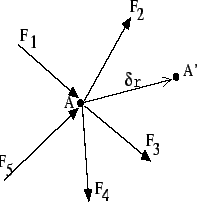Uma vez que o trabalho de uma força pode ser represntado a partir do produto escalar $W=F \cdot r$, podemos então representar a soma dos tabalhos das forças que atuam no ponto material do seguinte modo:

$$W_R = \sum_{i=1}^{n} F_i \cdot \delta_r$$ (9.1)

Com $n$ sendo igual ao número de forças que atuam sobre o ponto material. Uma vez que $\delta_r$ é constante, podemos reescrever a Equação (9.1) do seguinte modo:

$$W_R = \delta_r \sum_{i=1}^{n} F_i = F_R \cdot \delta_r$$ (9.2)

Uma vez que o sistema está em equilíbrio, temos que a força resultante $F_R$ deve ser nula, e portanto, teremos que:

$$W_R = F_R \cdot \delta_r = 0$$ (9.3)

A Equação (9.3) apenas expressa que o trabalho virtual das forças externas que atuam sobre um ponto material em equilíbrio, é nulo. Esse trabalho é chamado de virtual por que foi realizado sob um deslocamento virtual, ou seja, um deslocamento que não ocorre na realidade, que é apenas utilizado como artifício para a solução de determinados problemas em mecânica.

O princípio dos trabalhos virtuais pode ser aplicado a um corpo rígido com o seguinte enunciado: Se o corpo rígido está em equilíbrio, o trabalho virtual total de todas as forças externas que atuam sobre o corpo é nulo para qualquer deslocamento virtual realizado pelo corpo. Como em um corpo rígido o trabalho virtual das forças internas também é nulo, pode-se afirmar que para um corpo rígido em equilíbrio o trabalho virtual total devido as forças externas é igual ao trabalho virtual total devido as forças internas que atuam no corpo.