Equilíbrio de forças espaciais aplicadas em um ponto

Para que um ponto sujeito a forças espaciais esteja em equilíbrio, é necessário atender as seguintes equações:

$$\begin{array}{c} \\ R_x = \sum f_x = 0 \\ \\ R_y = \sum f_y = 0 \\ \\ R_z = \sum f_z = 0 \\ \\ \end{array}$$ (2.8)

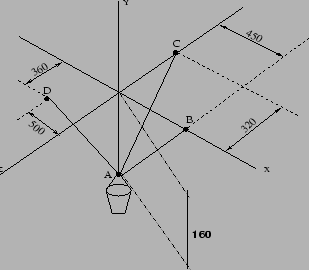Onde $R_x$ é o módulo da componente $x$ da resultante, e tal módulo é igual a soma dos módulos das componentes $x$ de todas as forças presentes no sistema. Do mesmo modo teremos os módulos $R_y$ e $R_z$. Vamos agora ao clássico problema do balde pendurado (Figura 2.6) para entender melhor o equilíbrio de forças espaciais aplicadas a um ponto.

Figure 2.6: Balde pendurado

Este problema consiste em determinar as trações nas cordas que sustentam o balde. Admitamos para esse problema que a massa do balde é de 20 Kg e que $\vec{g}=10\, m/s^2$.

A primeira coisa a fazer nesse problema é calcular os cossenos diretores das direções onde estão as forças. Para isso vamos utilizar o sistemas de eixos coordenados indicados na própria figura do prblema. O sentido das forças é arbitrário, PORÉM, o bom senso nos indica que as forças nas cordas tem sentido oposto ao da força peso, assim, vamos admitir que todas as forças ``apontam para cima'', exceto a força peso que ``aponta para baixo''.

Devemos lembrar também que o vetor $\vec{AB}$ é diferente do vetor $\vec{BA}$, o que é extremidade em um, é origem em outro, e como vimos anteriormente, os dois terão cossenos diretores diferentes. Lembrando de tudo isso vamos então calcular os cossenos diretores das direções AB, AC, AD e OA.

Um bom procedimento a ser adotado é definir inicialmente as coordenadas dos pontos, assim temos que:

Ponto	x	y	z
A	0	-160	0
B	450	0	0
C	0	0	320
D	-500	0	-360

Agora podemos calcular os cossenos diretores das direções AB, AC, AD e OA.

Direção	$\Delta_x$	$\Delta_y$	$\Delta_z$	$\vert\Delta\vert$	$\lambda_x$	$\lambda_y$	$\lambda_z$
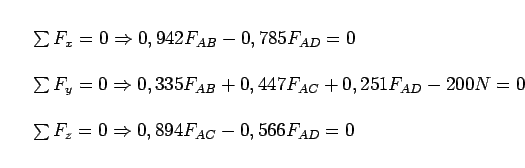AB	450	160	0	477,598	0,942	0,335	0,000
AC	0	160	320	357,771	0,000	0,447	0,894
AD	-500	160	-360	636,553	-0,785	0,251	-0,566
OA	0	-160	0	160,000	0,000	-1,000	0,000

Agora que temos os cossenos diretores das direções onde estão as forças envolvidas no problema, resta-nos equilibrar as componentes das forças nas direções x,y e z. Portanto, teremos que:

$$\begin{array}{l} \\ \sum F_x = 0 \Rightarrow 0,942 F_{AB}... ...ghtarrow 0,894 F_{AC} - 0,566 F_{AD} = 0 \\ \\ \end{array}$$ (2.9)

Resolvendo o sistema (2.9), teremos que:

$$\bgroup\color{black} \begin{array}{l} \\ F_{AB} = 204,960 ... ...;N \\ \\ F_{AD} = 245,952 \;N \\ \\ \end{array} \egroup$$

Simples, não é mesmo ?. Para obter o equlíbrio de forças espaciais aplicadas em um único ponto, basta fazer com que a soma vetorial de todos os vetores força aplicados a esse ponto seja nula. Preferencialmente trabalha-se com a representação analítica dos vetores, visto ser muito mais precisa que a abordagem gráfica, e extremamnete menos complicada do que as regras trigonométricas do seno e cosseno para os inúmeros triângulos envolvidos nesse problema.

Bom, apesar de em essência, o equilíbrio de forças espaciais aplicadas a um único ponto ser razoavelmente fácil, o exercício é indispensável, portanto, vamos nos exercitar um pouco resolvendo alguns problemas !